时间序列预测方法之 DeepAR

发表于 2019-10-09 更新于 2020-04-26 分类于调研分享阅读次数：

最近打算分享一些基于深度学习的时间序列预测方法。这是第一篇。

DeepAR 是 Amazon 于 2017 年提出的基于深度学习的时间序列预测方法，目前已集成到 Amazon SageMaker 和 GluonTS 中。前者是 AWS 的机器学习云平台，后者是 Amazon 开源的时序预测工具库。

传统的时间序列预测方法（ARIMA、Holt-Winters’ 等）往往针对一维时间序列本身建模，难以利用额外特征。此外，传统方法的预测目标通常是序列在每个时间步上的取值。与之相比，基于神经网络的 DeepAR 方法可以很方便地将额外的特征纳入考虑，且其预测目标是序列在每个时间步上取值的概率分布。在特定场景下，概率预测比单点预测更有意义。以零售业为例，若已知商品未来销量的概率分布，则可以利用运筹优化方法推算在不同业务目标下的最优采购量，从而辅助决策（详见《为什么需要考虑销量的随机性？》和《报童问题》）。

本文将简要地介绍一下 DeepAR 模型，并给出一个 demo。如果希望了解更多细节，建议直接阅读 Amazon 的论文 Deep AR: Probabilistic Forecasting with Autoregressive Recurrent Networks。

Model

用 $z_{i,t}$ 表示第 $i$ 个序列在时间步 $t$ 的值， $x_{i, t}$ 表示特征， $t_0$ 表示预测开始时刻。DeepAR 基于自回归循环神经网络预测 $z_{i,t}$ 的概率分布^[1]，用似然函数 $l(z_{i, t}|\theta_{i, t})$ 表示。

模型如下图所示，左边是训练过程，右边是预测过程。

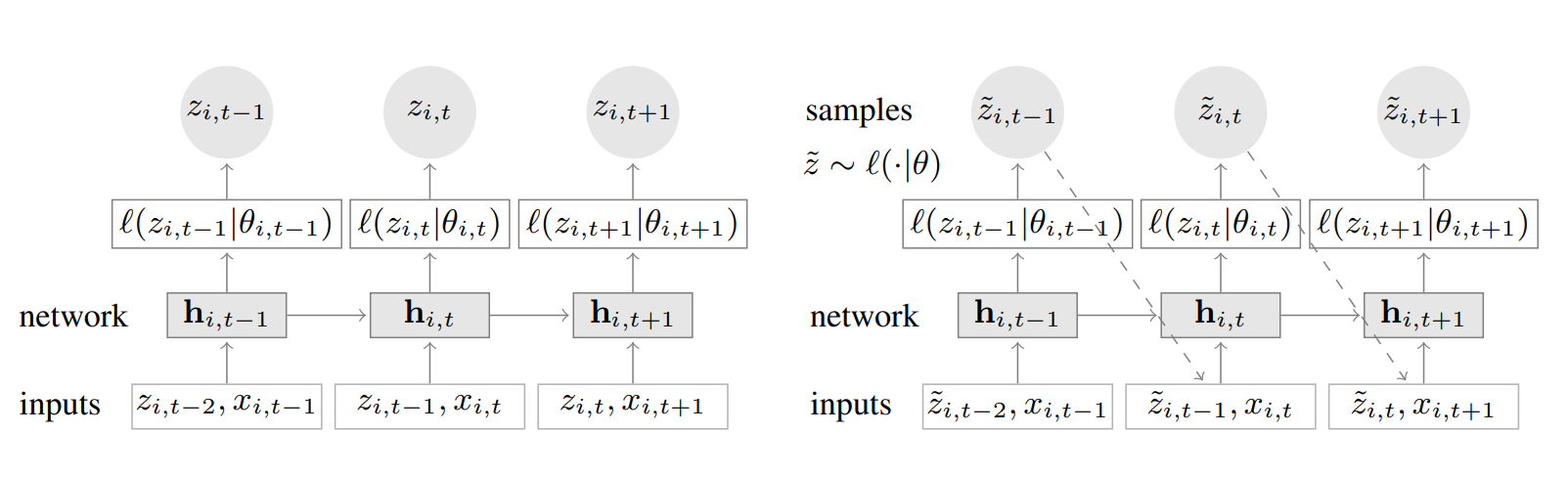
训练时，在每一个时间步 $t$ ，网络的输入包括特征 $x_{i, t}$ 、上一个时间步的取值 $z_{i, t-1}$ ，以及上一个时间步的状态 $\vec h_{i, t-1}$ 。先计算当前的状态 $\vec h_{i, t}=h(\vec h_{i, t-1}, z_{i, t-1}, x_{i, t})$ ，进而计算似然 $l(z|\theta)$ 的参数 $\theta_{i, t} = \theta(\vec h_{i, t})$ ，最后通过最大化对数似然

\mathcal L = \sum\limits_i\sum\limits_t\log l(z_{i,t}|\theta(\vec h_{i, t}))

来学习网络的参数。

训练完成后，将 $t<t_0$ 的历史数据喂入网络，获得初始状态 $\vec h_{i, t_0-1}$ ，就可以使用祖先采样（ancestral sampling）获取预测结果了：对于 $t_0, t_0+1, \cdots, T$ ，在每一个时间步随机采样得到 $\tilde z_{i,t}\sim l(\cdot|\theta_{i,t})$ ，这个采样值被作为下一个时间步的输入。重复这个过程，就可以得到一系列 $t_0\sim T$ 的采样值，利用这些采样值可以计算所需的目标值，如分位数、期望等。

$\theta(\vec h_{i, t})$ 的具体形式取决于似然函数 $l(z|\theta)$ ，而似然函数需要根据数据本身的统计特征来选择。如果选择 Gaussian 分布，则 $\theta=(\mu, \sigma)$ ，

\begin{aligned} l_G(z|\mu, \sigma) &= \frac{1}{\sqrt{2 \pi\sigma^2}}\exp\left(\frac{-(z- \mu)^2}{2\sigma^2}\right)\\ \mu(\vec h_{i,t}) &= \vec w_\mu^T\vec h_{i, t} + b_\mu\\ \sigma(\vec h_{i,t}) &= \log(1+\exp(\vec w_\sigma^T\vec h_{i, t} + b_\sigma)) \end{aligned}

对于计数类数据，可以使用负二项分布。

Code

Amazon 在 GluonTS 中提供了基于 MXNet 构建的 DeepAR 模型。由于不太熟悉 MXNet，这里提供一个基于 TensorFlow 构建的简单 demo。

模型和损失函数如下：

import tensorflow as tf
import tensorflow_probability as tfp

class DeepAR(tf.keras.models.Model):
    """
    DeepAR 模型
    """
    def __init__(self, lstm_units):
        super().__init__()
        # 注意，文章中使用了多层的 LSTM 网络，为了简单起见，本 demo 只使用一层
        self.lstm = tf.keras.layers.LSTM(lstm_units, return_sequences=True, return_state=True)
        self.dense_mu = tf.keras.layers.Dense(1)
        self.dense_sigma = tf.keras.layers.Dense(1, activation='softplus')

    def call(self, inputs, initial_state=None):
        outputs, state_h, state_c = self.lstm(inputs, initial_state=initial_state)

        mu = self.dense_mu(outputs)
        sigma = self.dense_sigma(outputs)
        state = [state_h, state_c]

        return [mu, sigma, state]

def log_gaussian_loss(mu, sigma, y_true):
    """
    Gaussian 损失函数
    """
    return -tf.reduce_sum(tfp.distributions.Normal(loc=mu, scale=sigma).log_prob(y_true))

实例化模型，指定优化器，就可以训练了：

LSTM_UNITS = 16
EPOCHS = 5

# 实例化模型
model = DeepAR(LSTM_UNITS)

# 指定优化器
optimizer = tf.keras.optimizers.Adam()

# 使用 RMSE 衡量误差
rmse = tf.keras.metrics.RootMeanSquaredError()

# 定义训练步
def train_step(x, y):
    with tf.GradientTape() as tape:
        mu, sigma, _ = model(x)
        loss = log_gaussian_loss(mu, sigma, y)
    grads = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(grads, model.trainable_variables))
    rmse(y, mu)

# 数据处理（略）
# train_data = do_something()

# 训练
for epoch in range(EPOCHS):
    for x, y in train_data:
        train_step(x, y)
    print('Epoch %d, RMSE %.4f' % (epoch + 1, rmse.result()))
    rmse.reset_states()

为了验证代码，我们随机生成一个带有周期的时间序列。下图展示了这个序列的一部分数据点。

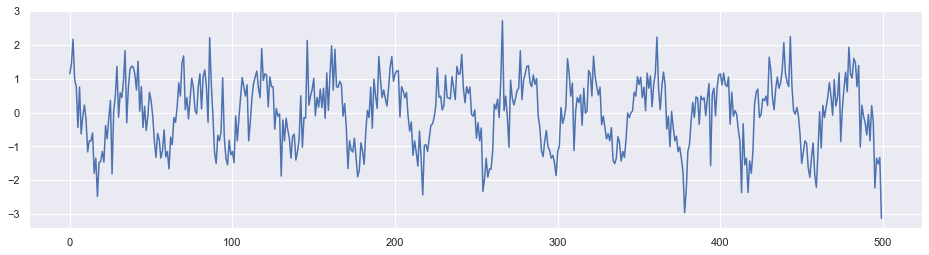
简单起见，我们没有加入额外的特征。

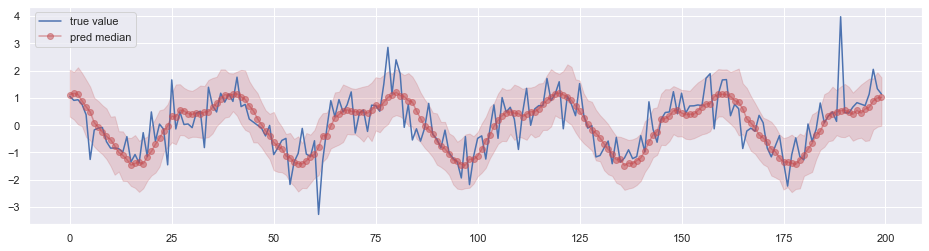
经过训练后用于预测，效果如下图所示，其中阴影部分表示 0.05 分位数 ~ 0.95 分位数的区间。

事实上也可以有其它的预测目标，例如分位数回归。 ↩︎