分位数回归

用 $Z$ 表示一个随机变量，其概率密度函数为 $f(z)$，累积分布函数为 $F(z)$。定义函数

$L(Z,\hat Z)=\rho\cdot\max(Z-\hat Z, 0)+(1-\rho)\cdot\max(\hat Z-Z, 0)$

其中 $\hat Z\in \mathbb R$，$\rho\in(0,1)$。求使得 $L(Z,\hat Z)$ 的期望最小的 $\hat Z$ 的取值。

$L(Z,\hat Z)$ 的期望为

$\begin{aligned} \mathbb{E}[L(Z,\hat Z)] &= \int_{-\infty}^{+\infty}L(z,\hat Z)f(z)\mathrm dz\\ &= \rho\int_{\hat Z}^{+\infty}(z-\hat Z)f(z)\mathrm dz + (1-\rho)\int_{-\infty}^{\hat Z}(\hat Z - z)f(z)\mathrm dz \end{aligned}$

令

$\begin{aligned} \frac{\partial \mathbb{E} [L(Z,\hat Z)]}{\partial \hat Z} &= 0\\ &=-\rho\int_{\hat Z} ^{+\infty}f(z)\mathrm dz+(1-\rho)\int_{-\infty}^{\hat Z}f(z)\mathrm dz\\ &=-\rho[1-F(\hat Z)]+(1-\rho)F(\hat Z)\\ &=F(\hat Z)-\rho \end{aligned}$

解得

$\hat Z^*=F^{-1}(\rho)$

即使得 $L(Z,\hat Z)$ 的期望最小的 $\hat Z$ 的取值为 $Z$ 的 $\rho$ 分位数。

在 DeepAR 等模型中，我们的预测目标是某个确定形式的概率分布的参数，通过最大化对数似然来优化网络。如果我们把预测的目标改为分位数，用 $L(\cdot)$ 作为损失函数呢？下图是实验的结果：

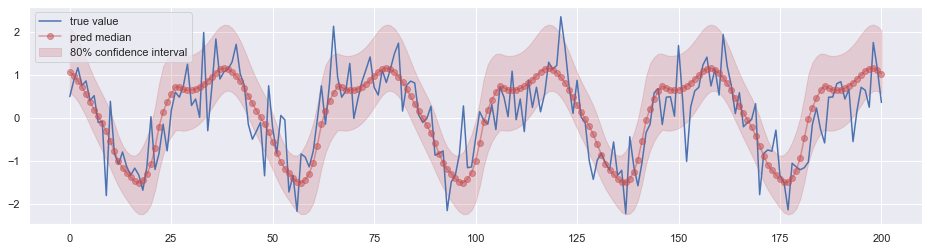
看起来也不错。且这种方式并不预先假设分布的具体形式，似乎更加通用一些。