小波变换简介

1. 傅里叶变换的局限性

傅里叶变换只能得到一个信号包含哪些频率成分，但无法从频域上得知信号在不同时间的频率信息，因此对频率会随着时间而改变的信号是无能为力的。举例来说：

import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft

t = np.linspace(0, 1, 400, endpoint=False)
cond = [t<0.25, (t>=0.25)&(t<0.5), t>=0.5]
f1 = lambda t: np.cos(2*np.pi*10*t)
f2 = lambda t: np.cos(2*np.pi*50*t)
f3 = lambda t: np.cos(2*np.pi*100*t)

y1 = np.piecewise(t, cond, [f1, f2, f3])
y2 = np.piecewise(t, cond, [f2, f1, f3])

Y1 = abs(fft(y1))
Y2 = abs(fft(y2))

plt.figure(figsize=(12, 9))
plt.subplot(221)
plt.plot(t, y1)
plt.title('signal_1 in time domain')
plt.xlabel('Time/second')

plt.subplot(222)
plt.plot(range(400), Y1)
plt.title('signal_1 in frequency domain')
plt.xlabel('Frequency/Hz')

plt.subplot(223)
plt.plot(t, y2)
plt.title('signal_2 in time domain')
plt.xlabel('Time/second')

plt.subplot(224)
plt.plot(range(400), Y2)
plt.title('signal_2 in frequency domain')
plt.xlabel('Frequency/Hz')

plt.tight_layout()
plt.show()

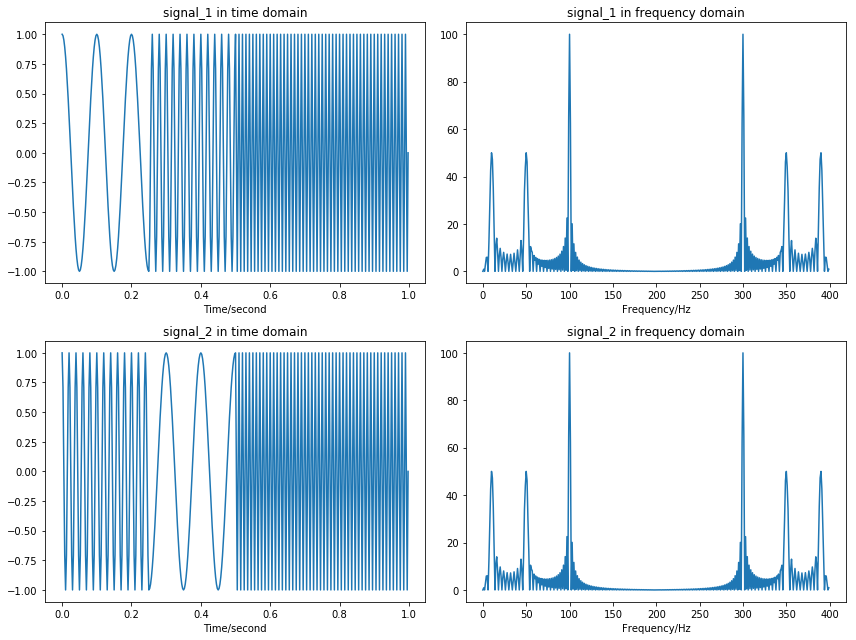
从时域上看相差很大的两个信号，在频域上却非常相近。无法从傅里叶变换得到的频域里得知某个频率是在哪个时间出现的。

一个很自然的思路是加窗，将长时间信号分成数个较短的等长信号，然后再分别对每个窗进行傅里叶变换，从而得到频率随时间的变化，这就是所谓的短时距傅里叶变换。这个做法的缺陷在于，窗函数越宽，频率的分辨率越好，但时间分辨率越差；反之，当窗函数越窄，时间的分辨率越好，但频率分辨率越差。

2. 连续小波变换

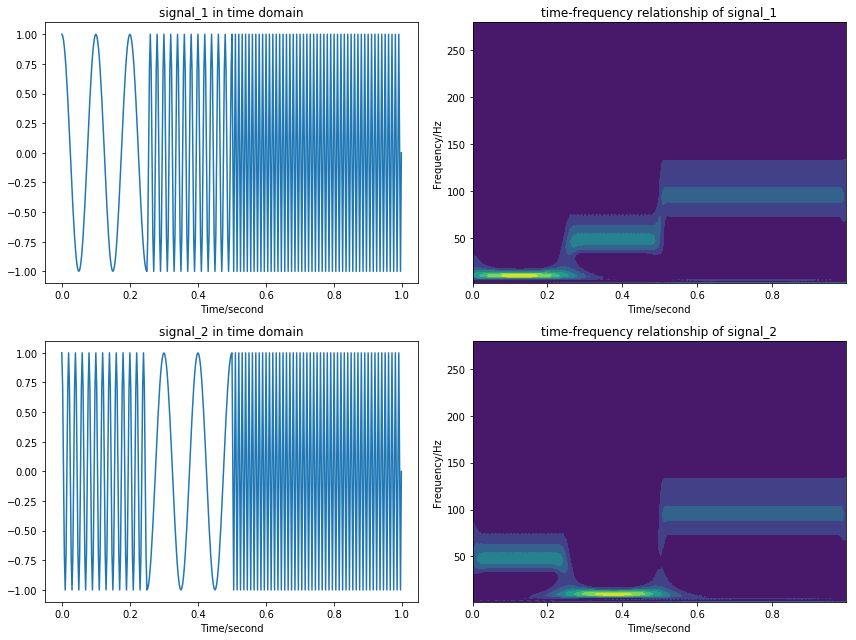
小波变换则可以解决这个问题。图2是对图1中的两个信号分别进行小波变换得到的时频关系。从图中不仅可以看到信号中有哪些频率，还可以看到不同的频率成分在什么时间出现。

小波函数定义为

$\psi_{a,b}(t) = \frac{1}{\sqrt a}\psi\left(\frac{t-b}{a}\right)$

其中 $a$ 是缩放因子，控制小波函数的伸缩；$b$ 是平移参数，控制小波函数的平移。缩放因子对应频率，平移参数对应时间。

$f(t)$ 在缩放因子为 $a$ 的子空间的投影为

$f_a(t) = \int_{-\infty}^{+\infty}W_f(a,b)\psi_{a,b}^*(t)\mathrm db$

其中小波系数为

$W_f(a, b) = \int_{-\infty}^{+\infty}f(t)\psi_{a,b}^*(t)\mathrm dt$

$^*$ 代表复共轭。

为了更直观地理解小波变换，先引入 Parseval 定理：

若 $f(t)$ 和 $g(t)$ 都是平方可积函数，则

$\int_{-\infty}^{+\infty} f(t)g^*(t)\mathrm dt = \frac1{2\pi}\int_{-\infty}^{+\infty}F(\omega)G^*(\omega)\mathrm d\omega$

其中 $F(\omega)=\mathcal F[f(t)]$，$G(\omega)=\mathcal F[g(t)]$

证明如下：

$\begin{aligned} \int_{-\infty}^{+\infty}f(t)g^*(t)\mathrm dt &=\int_{-\infty}^{+\infty}\left[\frac1{2\pi}\int_{-\infty}^{+\infty}F(\omega)\mathrm e^{i\omega t}\mathrm d\omega\right]g^*(t)\mathrm dt\\ &=\frac1{2\pi}\int_{-\infty}^{+\infty}F(\omega)\left[\int_{-\infty}^{+\infty}g^*(t)\mathrm e^{i\omega t}\mathrm dt\right]\mathrm d\omega\\ &=\frac1{2\pi}\int_{-\infty}^{+\infty}F(\omega)\left[\int_{-\infty}^{+\infty}g(t)\mathrm e^{-i\omega t}\mathrm dt\right]^*\mathrm d\omega\\ &= \frac1{2\pi}\int_{-\infty}^{+\infty}F(\omega)G^*(\omega)\mathrm d\omega \end{aligned}$

若 $f(t)$ 是信号，$g(t)=\psi_{a,b}(t)$ 是小波函数，则小波变换

$W_f(a,b) = \int_{-\infty}^{+\infty}f(t)\psi^*_{a,b}(t)\mathrm dt=\frac1{2\pi}\int_{-\infty}^{+\infty}F(\omega)\Psi^*_{a,b}(\omega)\mathrm d\omega$

从上式不难看出，只有当小波中心频率与原始信号固有频率接近的时候，小波系数才会取得极大值。因此，小波可以看作是一个只允许频率和小波中心频率相近的信号通过的带通滤波器。通过缩放因子可以得到一系列不同的中心频率，通过平移系数则可以检测时域上不同位置的信号。这样就得到了原信号在各个时间点包含的频率信息。

在 Python 中可以使用 pywt.cwt 实现连续小波变换。图2的结果就是由下面这段代码产生的。

import numpy as np
import matplotlib.pyplot as plt
import pywt

t = np.linspace(0, 1, 400, endpoint=False)
cond = [t<0.25, (t>=0.25)&(t<0.5), t>=0.5]
f1 = lambda t: np.cos(2*np.pi*10*t)
f2 = lambda t: np.cos(2*np.pi*50*t)
f3 = lambda t: np.cos(2*np.pi*100*t)

y1 = np.piecewise(t, cond, [f1, f2, f3])
y2 = np.piecewise(t, cond, [f2, f1, f3])

cwtmatr1, freqs1 = pywt.cwt(y1, np.arange(1, 200), 'cgau8', 1/400)
cwtmatr2, freqs2 = pywt.cwt(y2, np.arange(1, 200), 'cgau8', 1/400)

plt.figure(figsize=(12, 9))
plt.subplot(221)
plt.plot(t, y1)
plt.title('signal_1 in time domain')
plt.xlabel('Time/second')

plt.subplot(222)
plt.contourf(t, freqs1, abs(cwtmatr1))
plt.title('time-frequency relationship of signal_1')
plt.xlabel('Time/second')
plt.ylabel('Frequency/Hz')

plt.subplot(223)
plt.plot(t, y2)
plt.title('signal_2 in time domain')
plt.xlabel('Time/second')

plt.subplot(224)
plt.contourf(t, freqs2, abs(cwtmatr2))
plt.title('time-frequency relationship of signal_2')
plt.xlabel('Time/second')
plt.ylabel('Frequency/Hz')

plt.tight_layout()
plt.show()

3. 离散小波变换

离散小波变换顾名思义就是离散的输入以及离散的输出，但是这里并没有一个简单而明确的公式来表示输入及输出的关系，只能以阶层式架构来表示。

Python 中可以使用 pywt.dwt实现离散小波变换：

import numpy as np
import matplotlib.pyplot as plt
import pywt

y = pywt.data.ecg()
x = range(len(y))

ca, cd = pywt.dwt(y, 'db4')
ya = pywt.idwt(ca, None, 'db4') # approximated component
yd = pywt.idwt(None, cd, 'db4') # detailed component

plt.figure(figsize=(12,9))
plt.subplot(311)
plt.plot(x, y)
plt.title('original signal')
plt.subplot(312)
plt.plot(x, ya)
plt.title('approximated component')
plt.subplot(313)
plt.plot(x, yd)
plt.title('detailed component')
plt.tight_layout()
plt.show()

上面的代码将原信号分解为一个低频的近似分量和一个高频的细节分量：

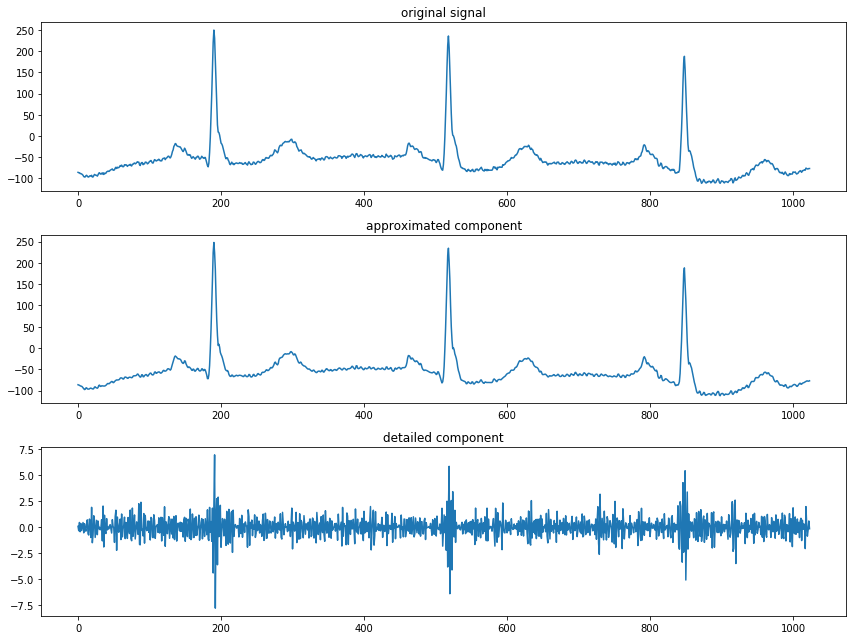
也可以使用 pywt.wavedec 直接进行多阶小波分解：

import numpy as np
import matplotlib.pyplot as plt
import pywt

y = pywt.data.ecg()
x = range(len(y))

coeffs = pywt.wavedec(y, 'db4', level=4) # 4阶小波分解

ya4 = pywt.waverec(np.multiply(coeffs, [1, 0, 0, 0, 0]).tolist(), 'db4')
yd4 = pywt.waverec(np.multiply(coeffs, [0, 1, 0, 0, 0]).tolist(), 'db4')
yd3 = pywt.waverec(np.multiply(coeffs, [0, 0, 1, 0, 0]).tolist(), 'db4')
yd2 = pywt.waverec(np.multiply(coeffs, [0, 0, 0, 1, 0]).tolist(), 'db4')
yd1 = pywt.waverec(np.multiply(coeffs, [0, 0, 0, 0, 1]).tolist(), 'db4')

plt.figure(figsize=(12, 12))
plt.subplot(611)
plt.plot(x, y)
plt.title('original signal')
plt.subplot(612)
plt.plot(x, ya4)
plt.title('approximated component in level 4')
plt.subplot(613)
plt.plot(x, yd4)
plt.title('detailed component in level 4')
plt.subplot(614)
plt.plot(x, yd3)
plt.title('detailed component in level 3')
plt.subplot(615)
plt.plot(x, yd2)
plt.title('detailed component in level 2')
plt.subplot(616)
plt.plot(x, yd1)
plt.title('detailed component in level 1')
plt.tight_layout()
plt.show()

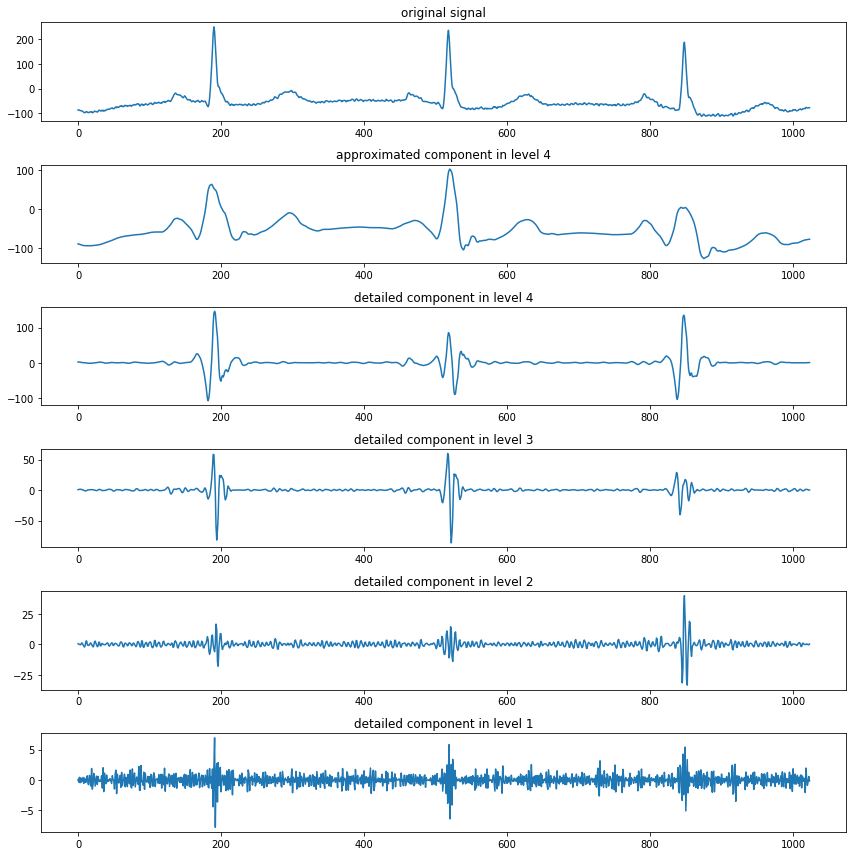
上面的代码将原信号分解为一个低频的近似分量和四个高频的细节分量：

参考文献

1. 小波与傅里叶分析基础（第二版）， 电子工业出版社，2017.6
2. Wavelet - Wikipedia
3. 知乎专栏 - 时频分析与小波变换
4. PyWavelets - Wavelet Transforms in Python