傅里叶变换简介

发表于 更新于 分类于

1. 傅里叶级数 Fourier Series (FS)

傅里叶级数得名于法国数学家约瑟夫·傅里叶，他提出任何函数都可以展开为三角级数。

考虑一个在区间 [t0,t0+T][t_0, t_0+T] 上可积的函数 f(t)f(t)，其傅里叶级数为

f(t)=a02+∑n=1∞(ancos⁡2πnTt+bnsin⁡2πnTt)(1)f(t) = \dfrac{a_0}2 + \sum\limits_{n=1}^\infty\left(a_n\cos\dfrac{2\pi n}Tt + b_n\sin\dfrac{2\pi n}Tt\right) \tag{1}

其中

an=2T∫t0t0+Tf(t)cos⁡2πnTtdt,n=0,1,2,⋯(2)a_n = \dfrac2T\int_{t_0}^{t_0+T}f(t)\cos\dfrac{2\pi n}Tt\mathrm{d}t, n=0, 1, 2, \cdots \tag{2}

bn=2T∫t0t0+Tf(t)sin⁡2πnTtdt,n=1,2,⋯(3)b_n = \dfrac2T\int_{t_0}^{t_0+T}f(t)\sin\dfrac{2\pi n}Tt\mathrm{d}t, n=1, 2, \cdots \tag{3}

由欧拉公式 eiθ=cos⁡θ+isin⁡θ\mathrm{e}^{i\theta} = \cos\theta+i\sin\theta 得

cos⁡θ=12(eiθ+e−iθ)sin⁡θ=−i2(eiθ−e−iθ)(4)\begin{aligned} \cos\theta &= \dfrac12\left(\mathrm{e}^{i\theta}+\mathrm{e}^{-i\theta}\right)\\ \sin\theta &= -\dfrac i2\left(\mathrm{e}^{i\theta}-\mathrm{e}^{-i\theta}\right) \end{aligned} \tag{4}

代入（1）可得

f(t)=a02+∑n=1∞(an−ibn2ei2πnTt+an+ibn2e−i2πnTt)(5)f(t) = \dfrac{a_0}2 + \sum\limits_{n=1}^\infty\left(\dfrac{a_n-ib_n}2\mathrm{e}^{i\frac{2\pi n}Tt} + \dfrac{a_n+ib_n}2\mathrm{e}^{-i\frac{2\pi n}Tt}\right) \tag{5}

令

cn={an−ibn2n>0a02n=0a∣n∣+ib∣n∣2n<0(6)c_n = \begin{cases} \dfrac{a_n - ib_n}2 &\text{n>0}\\ \dfrac{a_0}2 &\text{n=0}\\ \dfrac{a_{|n|} + ib_{|n|}}2 &\text{n<0} \end{cases} \tag{6}

则可以得到傅里叶级数的复数形式

f(t)=∑n=−∞+∞cnei2πnTt(7)f(t) = \sum\limits_{n=-\infty}^{+\infty}c_n\mathrm{e}^{i\frac{2\pi n}Tt}\tag{7}

其中

cn=1T∫t0t0+Tf(t)e−i2πnTtdt,n=0,±1±2,⋯(8)c_n = \dfrac1T\int_{t_0}^{t_0+T}f(t)\mathrm{e}^{-i\frac{2\pi n}Tt}\mathrm{d}t, \qquad n=0, \pm1 \pm2,\cdots\tag{8}

2. 傅里叶变换 Fourier Transform (FT)

傅里叶变换可以看作傅里叶级数的连续形式。

首先考虑定义在 [−T2,T2][-\frac T2, \frac T2] 上的函数的傅里叶级数展开：

f(t)=∑n=−∞+∞cnei2πnTt(9)f(t) = \sum\limits_{n=-\infty}^{+\infty}c_n\mathrm{e}^{i\frac{2\pi n}Tt}\tag{9}

其中

cn=1T∫−T/2T/2f(t)e−i2πnTtdt,n=0,±1±2,⋯(10)c_n = \dfrac1T\int_{-T/2}^{T/2}f(t)\mathrm{e}^{-i\frac{2\pi n}Tt}\mathrm{d}t, \qquad n=0, \pm1 \pm2,\cdots\tag{10}

令

Δω=2πT(11)\Delta\omega=\dfrac{2\pi}T\tag{11}

记

f^(nΔω)=Tcn=∫−T/2T/2f(t)e−inΔωtdt,n=0,±1,±2,⋯(12)\hat{f}(n\Delta\omega)=Tc_n=\int_{-T/2}^{T/2}f(t)\mathrm{e}^{-in\Delta\omega t}\mathrm{d}t, \qquad n=0, \pm1, \pm2, \cdots\tag{12}

则

cn=f^(nΔω)T=Δω2πf^(nΔω)(13)c_n=\dfrac{\hat{f}(n\Delta\omega)}T=\dfrac{\Delta\omega}{2\pi}\hat{f}(n\Delta\omega)\tag{13}

f(t)=∑n=−∞+∞cnei2πnTt=12π∑n=−∞+∞f^(nΔω)einΔωtΔω(14)\begin{aligned} f(t) &= \sum\limits_{n=-\infty}^{+\infty}c_n\mathrm{e}^{i\frac{2\pi n}Tt} \\ &= \dfrac1{2\pi} \sum\limits_{n=-\infty}^{+\infty}\hat{f}(n\Delta\omega)\mathrm{e}^{in\Delta\omega t}\Delta\omega \end{aligned} \tag{14}

当 T→∞T\to\infty 时，nΔω→ωn\Delta\omega\to\omega，Δω→dω\Delta\omega\to\mathrm{d}\omega， (14) 中的求和变为积分

f(t)=12π∫−∞+∞f^(ω)eiωtdω(15)f(t) = \dfrac1{2\pi}\int_{-\infty}^{+\infty}\hat{f}(\omega)\mathrm{e}^{i\omega t}\mathrm{d}\omega\tag{15}

相应地，(12) 变为

f^(ω)=∫−∞+∞f(t)e−iωtdt(16)\hat{f}(\omega)=\int_{-\infty}^{+\infty}f(t)\mathrm{e}^{-i\omega t}\mathrm{d}t\tag{16}

(16) 称为傅里叶变换，记作 f^(ω)=F[f](t)\hat{f}(\omega) = \mathcal F[f](t)；(15) 称为傅里叶变换的逆变换，记作 f(t)=F−1[f^](ω)f(t) = \mathcal F^{-1}[\hat{f}](\omega)。在信号分析中，f(t)f(t) 称为信号的时域表示，f^(ω)\hat{f}(\omega) 称为信号的频域表示。

需要明确的是，不管是用时域还是用频域来表示一个信号，它们代表的都是同一个信号。可以从线性空间的角度理解这一点。同一个信号在不同的表象（或者说基向量）下具有不同的坐标。同一个向量在不同表象下的坐标可以通过一个线性变换联系起来。如果是有限维的空间，这个线性变换可以表示为一个矩阵。而傅里叶变换则是无限维空间不同表象之间的一种变换。举例来说，在量子力学中，一个波函数的坐标表象到动量表象间的变换就是一个傅里叶变换。

也可以将角频率 ω\omega 替换为自然频率 ν\nu，有 ω=2πν\omega = 2\pi\nu，则

f^(ν)=Ff(t)=∫−∞+∞f(t)e−i2πνtdt(17)\hat{f}(\nu) =\mathcal Ff(t)= \int_{-\infty}^{+\infty}f(t)\mathrm{e}^{-i2\pi\nu t}\mathrm{d}t\tag{17}

f(t)=F−1f^(ν)=∫−∞+∞f^(ξ)ei2πνtdν(18)f(t) =\mathcal F^{-1}\hat{f}(\nu) = \int_{-\infty}^{+\infty}\hat{f}(\xi)\mathrm{e}^{i2\pi\nu t}\mathrm{d}\nu\tag{18}

3. 离散时间傅里叶变换 Discrete-time Fourier Transform (DTFT)

一般情况下，我们处理的信号都是离散的。取 f(t)f(t) 在时间上的离散采样

fn=f(nτ),n=0,±1,±2,⋯(19)f_n = f(n\tau), \qquad n=0, \pm1, \pm2, \cdots\tag{19}

τ\tau 是采样的时间间隔。傅里叶变换只能作用在连续函数上，为此我们引入

fs(t)=f(t)∑n=−∞+∞δ(t−nτ)=∑n=−∞+∞f(t)δ(t−nτ)=∑n=−∞+∞fnδ(t−nτ)(20)\begin{aligned} f_s(t) &= f(t)\sum\limits_{n=-\infty}^{+\infty}\delta(t-n\tau)\\ &=\sum\limits_{n=-\infty}^{+\infty}f(t)\delta(t-n\tau)\\ &=\sum\limits_{n=-\infty}^{+\infty}f_n\delta(t-n\tau) \end{aligned} \tag{20}

其中

δ(x)={+∞,x=00,x≠0(21)\delta(x) = \begin{cases} +\infty, &x=0\\ 0, &x\neq0 \end{cases} \tag{21}

为 Dirac 函数。∑n=−∞+∞δ(t−nτ)\sum\limits_{n=-\infty}^{+\infty}\delta(t-n\tau) 称为 Dirac 梳子，亦称 Shah 分布，是一个采样函数，常用在数字信号处理和离散时间信号分析中。

对 fs(t)f_s(t) 作傅里叶变换

f^s(ω)=∫−∞+∞fs(t)e−iωtdt=∫−∞+∞∑n=−∞+∞f(t)δ(t−nτ)e−iωtdt=∑n=−∞+∞∫−∞+∞δ(t−nτ)f(t)e−iωtdt=∑n=−∞+∞fne−iωnτ(22)\begin{aligned} \hat{f}_s(\omega)&=\int_{-\infty}^{+\infty}f_s(t)\mathrm{e}^{-i\omega t}\mathrm{d}t\\ &=\int_{-\infty}^{+\infty}\sum\limits_{n=-\infty}^{+\infty}f(t)\delta(t-n\tau)\mathrm{e}^{-i\omega t}\mathrm{d}t\\ &=\sum\limits_{n=-\infty}^{+\infty}\int_{-\infty}^{+\infty}\delta(t-n\tau)f(t)\mathrm{e}^{-i\omega t}\mathrm{d}t\\ &=\sum\limits_{n=-\infty}^{+\infty}f_n\mathrm{e}^{-i\omega n\tau} \end{aligned} \tag{22}

这里利用了 Dirac 函数的性质 ∫−∞+∞δ(x)g(x)dx=g(0)\int_{-\infty}^{+\infty}\delta(x)g(x)\mathrm dx=g(0)。(22) 即为离散时间傅里叶变换。

下面简单介绍一下采样定理。若原信号 f(t)f(t) 不包含高于 Ωm\Omega_m 的频率，即 f^(ω)=0,∀∣ω∣>Ωm\hat{f}(\omega) = 0,\forall |\omega| > \Omega_m，则只要采样频率 ωs≥2Ωm\omega_s\geq2\Omega_m，时域采样就能完全重建原信号。

将 f^(ω)\hat{f}(\omega) 在 [−ωs2,ωs2][-\frac{\omega_s}2, \frac{\omega_s}2] 上展开为傅里叶级数

f^(ω)=∑m=−∞+∞cmei2πmωsω(23)\hat{f}(\omega) = \sum\limits_{m=-\infty}^{+\infty}c_m\mathrm e^{i\frac{2\pi m}{\omega_s}\omega}\tag{23}

其中

cm=1ωs∫−ωs/2ωs/2f^(ω)e−i2πmωsωdω(24)c_m = \frac 1{\omega_s}\int_{-\omega_s/2}^{\omega_s/2}\hat{f}(\omega)\mathrm e^{-i\frac{2\pi m}{\omega_s}\omega}\mathrm d\omega\tag{24}

注意到 ∣ω∣>Ωm|\omega|>\Omega_m 时 f^(ω)=0\hat{f}(\omega) = 0，而 ωs≥2Ωm\omega_s\geq2\Omega_m，故 ∣ω∣>ωs/2|\omega|>\omega_s/2 时 f^(ω)=0\hat{f}(\omega) = 0，因此 (24) 可改写为

cm=1ωs∫−∞+∞f^(ω)e−i2πmωsωdω=2πωsf(−2πωsm)=τf(−mτ)=τf−m(25)\begin{aligned} c_m &= \frac 1{\omega_s}\int_{-\infty}^{+\infty}\hat{f}(\omega)\mathrm e^{-i\frac{2\pi m}{\omega_s}\omega}\mathrm d\omega\\ &=\frac{2\pi}{\omega_s}f(-\frac{2\pi}{\omega_s}m)\\ &=\tau f(-m\tau)\\ &=\tau f_{-m} \end{aligned} \tag{25}

代入 (23)，得

f^(ω)=∑m=−∞+∞τf−mei2πmωsω=∑n=−∞+∞τfne−i2πnωsω=τ∑n=−∞+∞fne−iωnτ=τf^s(ω)(26)\begin{aligned} \hat{f}(\omega) &= \sum\limits_{m=-\infty}^{+\infty}\tau f_{-m}\mathrm e^{i\frac{2\pi m}{\omega_s} \omega}\\ &= \sum\limits_{n=-\infty}^{+\infty}\tau f_{n}\mathrm e^{-i\frac{2\pi n}{\omega_s}\omega}\\ &= \tau\sum\limits_{n=-\infty}^{+\infty}f_n\mathrm{e}^{-i\omega n\tau }\\ &= \tau\hat{f}_s(\omega) \end{aligned} \tag{26}

这里 n=−mn=-m。(26) 说明原信号的傅里叶变换可以由采样信号确定，进而可以利用傅里叶逆变换重建原信号。

此外，不难发现

f^s(ω)=∑n=−∞+∞fne−iωnτ=∑n=−∞+∞fne−i2πnωωs(27)\begin{aligned} \hat{f}_s(\omega) &= \sum\limits_{n=-\infty}^{+\infty}f_n \mathrm{e}^{-i\omega n\tau } \\ &= \sum\limits_{n=-\infty}^{+\infty}f_n\mathrm{e}^{-i2\pi n\frac \omega{\omega_s}} \end{aligned} \tag{27}

是一个周期为 ωs\omega_s 的周期函数。离散傅里叶变换f^s(ω)\hat{f}_s(\omega)可以看作原信号连续傅里叶变换f^(ω)\hat{f}(\omega)的周期延拓，时域的离散化造成了频域的周期化。

4. 离散傅里叶变换 Discrete Fourier Transform (DFT)

离散时间傅里叶变换在频域上仍然是连续的。如果把频域也离散化，就得到了离散傅里叶变换。

f^k=∑n=0N−1fne−i2πNnk,k=0,1,⋯ ,N−1(28)\hat{f}_k = \sum\limits_{n=0}^{N-1}f_n\mathrm{e}^{-i\frac{2\pi}Nnk}, \qquad k=0, 1, \cdots, N-1\tag{28}

也可以写成矩阵形式

[f^0f^1f^2⋮f^N−1]=[111⋯11φφ2⋯φN−11φ2φ4⋯φ2(N−1)⋮⋮⋮⋱⋮1φN−1φ2(N−1)⋯φ(N−1)2][f0f1f2⋮fN−1](29)\left[ \begin{matrix} \hat{f}_0\\ \hat{f}_1\\ \hat{f}_2\\ \vdots\\ \hat{f}_{N-1} \end{matrix} \right] =\left[ \begin{matrix} 1 & 1 & 1 & \cdots & 1\\ 1 & \varphi & \varphi^2 & \cdots & \varphi^{ N-1}\\ 1 & \varphi^2 &\varphi^4 & \cdots & \varphi^{2(N-1)}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \varphi^{N-1} & \varphi^{2(N-1)} & \cdots & \varphi^{(N-1)^2} \end{matrix} \right] \left[ \begin{matrix} f_0\\ f_1\\ f_2\\ \vdots\\ f_{N-1} \end{matrix} \right] \tag{29}

其中 φ=e−i2π/N\varphi=\mathrm e^{-i2\pi/N}。

离散傅里叶变换的逆变换为

fn=1N∑k=0N−1f^kei2πNnk,n=0,1,⋯ ,N−1(30)f_n = \frac{1}{N}\sum\limits_{k=0}^{N-1}\hat{f}_k\mathrm e^{i\frac{2\pi}{N}nk}, \qquad n=0, 1, \cdots, N-1 \tag{30}

5. 快速傅里叶变换 Fast Fourier Transform (FFT)

直接根据定义计算离散傅里叶变换的复杂度是 O(N2)O(N^2)。快速傅里叶变换是快速计算离散傅里叶变换及其逆变换的一类数值算法。FFT 通过把 DFT 矩阵分解为稀疏矩阵之积，能够将复杂度降低到 O(Nlog⁡N)O(N\log N)。

在 Python 中可以利用 scipy.fftpack 进行快速傅里叶变换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from scipy.fftpack import fft, ifft

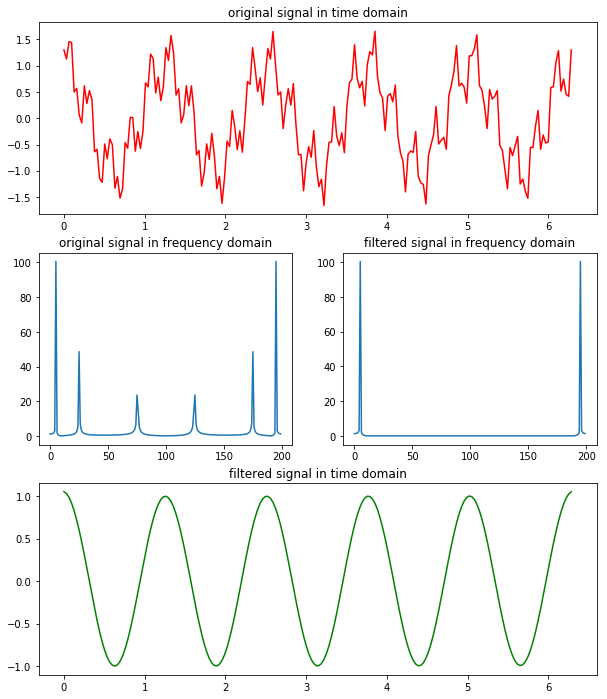
x = np.linspace(0, 2*np.pi, 200) # 采样频率为 200Hz
y = np.cos(5*x) + 0.5*np.sin(25*x) + 0.3*np.cos(75*x) # 根据采样定理，信号中不能包含超过 100Hz 的频率成分
plt.figure(figsize=(10,12))
ax1 = plt.subplot(311)
ax1.plot(x, y, 'r')
ax1.set_title('original signal in time domain')

Y = fft(y) # 快速傅里叶变换，得到频域
ax2 = plt.subplot(323)
ax2.plot(range(200), abs(Y))
ax2.set_title('original signal in frequency domain')

Y[10:-9] = 0 # 滤波
ax3 = plt.subplot(324)
ax3.plot(range(200), abs(Y))
ax3.set_title('filtered signal in frequency domain')

filtered = ifft(Y).real # 逆变换，得到滤波后的时域信号
ax4 = plt.subplot(313)
ax4.plot(x, filtered, 'g')
ax4.set_title('filtered signal in time domain')

参考文献

  1. 小波与傅里叶分析基础（第二版）， 电子工业出版社，2017.6
  2. Fourier transform - Wikipeida
  3. Discrete-time Fourier transform - Wikipedia
  4. Discrete Fourier transform - Wikipedia
  5. Discrete Fourier transforms (scipy.fftpack)