时间序列预测方法之 Transformer

发表于 2019-10-29 更新于 2020-04-26 分类于调研分享阅读次数：

最近打算分享一些基于深度学习的时间序列预测方法。这是第三篇。

前面介绍的 DeepAR 和 DeepState 都是基于 RNN 的模型。RNN 是序列建模的经典方法，它通过递归来获得序列的全局信息，代价是无法并行。CNN 也可以用来建模序列，但由于卷积捕捉的是局部信息，CNN 模型往往需要通过叠加很多层才能获得较大的感受野。后续我可能会 ~~(意思就是未必会)~~ 介绍基于 CNN 的时间序列预测方法。Google 在 2017 年发表的大作 Attention Is All You Need 为序列建模提供了另一种思路，即单纯依靠注意力机制（Attention Mechanism），一步到位获得全局信息。Google 将这个模型称为 Transformer。Transformer 在自然语言处理、图像处理等领域都取得了很好的效果。Transformer 的结构如下图所示（误

今次要介绍的是一篇 NIPS 2019 的文章 Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting，该文章将 Transformer 模型应用到时间序列预测中^[1]，并提出了一些改进方向。

我们首先介绍注意力机制，然后简单介绍一下模型，最后给出一个 demo。

Attention

根据 Google 的方案，Attention 定义为

\mathrm{Attention}(Q, K, V) = \mathrm{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V

其中 $Q\in\mathbb R^{n\times d_k}$ ， $K\in\mathbb R^{m\times d_k}$ ， $V\in\mathbb R^{m\times d_v}$ 。从矩阵的维度信息来看，可以认为 Attention 把一个 $n\times d_k$ 的序列 $Q$ 编码成一个 $n\times d_v$ 的新序列。记 $Q = [q_1, q_2, \cdots, q_n]^\top$ ， $K = [k_1, k_2, \cdots, k_m]^\top$ ， $V = [v_1, v_2, \cdots, v_m]^\top$ ，可以看到 $k$ 和 $v$ 是一一对应的。单看 $Q$ 中的每一个向量，有

\mathrm{Attention}(q_t, K, V) = \sum\limits_{s=1}^m\frac 1Z\exp\left(\frac{q_t k_s^\top}{\sqrt{d_k}}\right)v_s\qquad t=0, 1, \cdots, n

其中 $Z$ 是 softmax 函数的归一化因子。从上式可以看出，每一个 $q_t$ 都被编码成了 $v_1, v_2, \cdots, v_m$ 的加权和， $v_s$ 所占的权重取决于 $q_t$ 与 $k_s$ 的内积（点乘）。缩放因子 $\sqrt{d_k}$ 起到一定的调节作用，避免内积很大时 softmax 的梯度很小。这种定义下的注意力机制被称为缩放点乘注意力（Scaled Dot-Product Attention）。

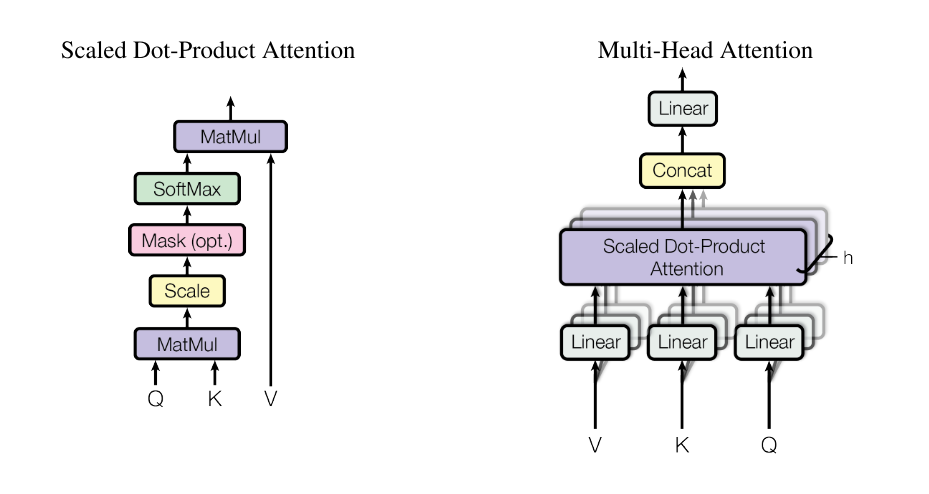
在 Attention 的基础上，Google 又提出了 Multi-Head Attention，其定义如下

\begin{aligned} \mathrm{MultiHead}(Q, K, V) &= \mathrm{Concat}(head_1, head_2, \cdots, head_h)\\ head_i &= \mathrm{Attention} (Q_i,K_i,V_i )\\ Q_i &= QW_i^Q\\ K_i &= KW_i^K\\ V_i &= VW_i^V \end{aligned}

其中 $W_i^Q,W_i^K\in\mathbb R^{d_k\times\tilde{d_k}}$ ， $W_i^V\in\mathbb R^{d_v\times\tilde{d_v}}$ 。简单来说，就是把 $Q$ 、 $K$ 和 $V$ 通过线性变换映射到不同的表示空间，然后计算 Attention；重复 $h$ 次，把得到的 $h$ 个 Attention 的结果拼接起来，最后输出一个 $n\times (h\tilde{d_v})$ 的序列。

在 Transformer 中，大部分的 Attention 都是 Self Attention（“自注意力”或“内部注意力”），就是在一个序列内部做 Attention，亦即 $\mathrm{Attention}(X,X,X)$ 。更准确地说，是 Multi-Head Self Attention，即 $\mathrm{MultiHead}(X,X,X)$ 。Self Attention 可以理解为寻找序列 $X$ 内部不同位置之间的联系。

Model

前面讲的基本上都是 Google 那篇 Transformer 文章的内容，现在我们回到时序预测这篇文章。为了避免混淆，我们用 Time Series Transformer 指代后者^[2]。

先回顾一下之前介绍的 DeepAR 模型：假设每个时间步的目标值 $z_t$ 服从概率分布 $l(z_t|\theta_t)$ ；先使用 LSTM 单元计算当前时间步的隐态 $h_t = \mathrm{LSTM}(h_{t-1}, z_{t-1}, x_t)$ ，再计算概率分布的参数 $\theta_t = \theta(h_t)$ ，最后通过最大化对数似然 $\sum_t \log l(z_t|\theta_t)$ 来学习网络参数。Time Series Transformer 的网络结构与 DeepAR 类似，只是将 LSTM 层替换为 Multi-Head Self Attention 层，从而不需要递归，而是一次性计算所有时间步的 $\theta_t$ 。如下图所示^[3]：

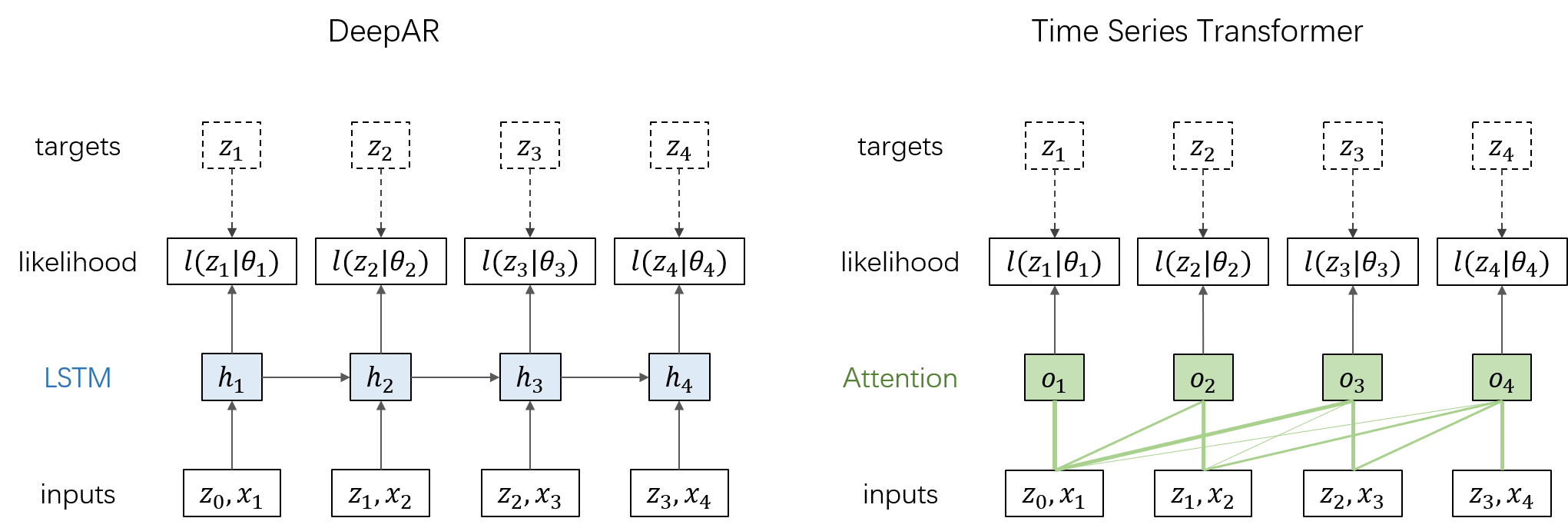
需要注意的是，对当前时间步做预测时，只能利用截止到当前时间步的输入。因此，在计算 Attention 时需要增加一个 Mask，将矩阵 $QK^\top$ 的上三角元素置为 $-\infty$ 。

在此基础上，文章对模型又做了两个改进。

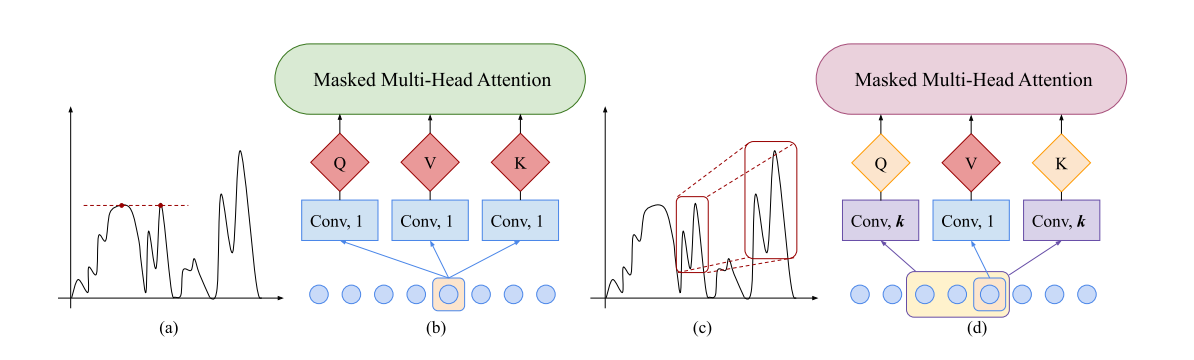
第一个改进点叫做 Enhancing the locality of Transformer，字面意思就是增强 Transformer 的局域性。时间序列中通常会有一些异常点，一个观测值是否应该被视作异常相当程度上取决于它所处的上下文环境。而 Multi-Head Self Attention

head_i = \mathrm{softmax}\left(\frac{Q_iK_i^\top}{\sqrt{\tilde{d_k}}}\cdot mask\right)V_i\\ Q_i = XW_i^Q,\quad K_i = XW_i^K,\quad V_i = XW_i^V\\

在计算序列内部不同位置的关系时，并没有考虑各个位置所处的局域环境，这会使预测容易受异常值的干扰。在博客的开头我们已经提到卷积操作可以用来捕捉局部信息。如果在计算 $Q_i$ 和 $K_i$ 时使用卷积代替线性变换，就可以在 Self Attention 中引入局部信息。注意，由于当前时间步不能使用未来的信息，这里使用的是因果卷积（causal convolution）。~~后续介绍基于 CNN 的时序预测时，因果卷积还会扮演重要角色。~~

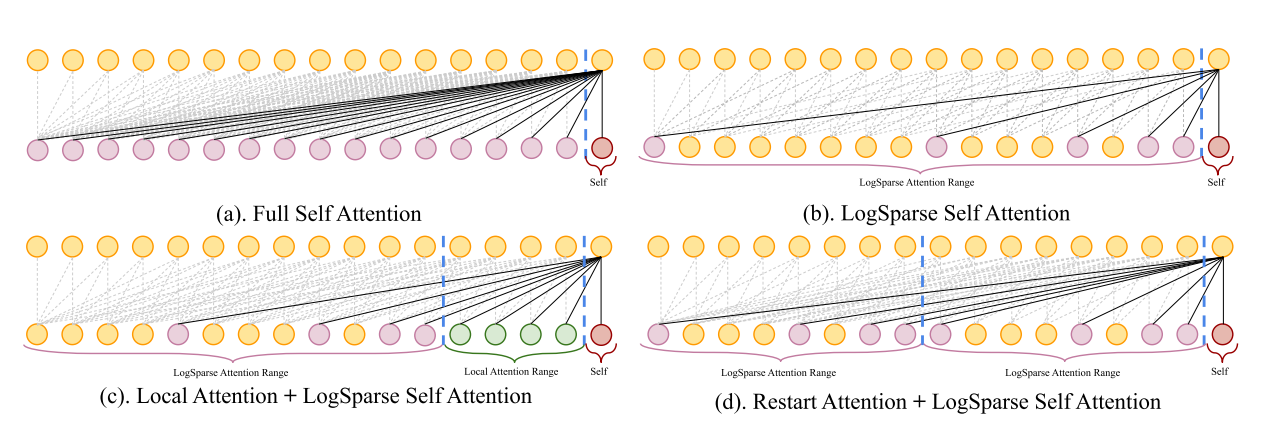
第二个改进点叫做 Breaking the memory bottleneck of Transformer. 假设序列长度为 $n$ ，Self Attention 的计算量为 $O(n^2)$ 。在时序预测中，往往要考虑长程依赖，这种情况下 memory usage 就会比较可观了。针对这一问题，文章提出了 LogSparse Self Attention 结构，使计算量减少到 $O(n(\log n)^2)$ ，如下图所示。

Code

按照惯例，这里给出一个基于 TensorFlow 的简单 demo。需要说明的是，本 demo 没有实现 LogSparse Self Attention。

以下定义了 Attention 层和 Transformer 模型：

import tensorflow as tf

class Attention(tf.keras.layers.Layer):
    """
    Multi-Head Convolutional Self Attention Layer
    """
    def __init__(self, dk, dv, num_heads, filter_size):
        super().__init__()
        self.dk = dk
        self.dv = dv
        self.num_heads = num_heads
        
        self.conv_q = tf.keras.layers.Conv1D(dk * num_heads, filter_size, padding='causal')
        self.conv_k = tf.keras.layers.Conv1D(dk * num_heads, filter_size, padding='causal')
        self.dense_v = tf.keras.layers.Dense(dv * num_heads)
        self.dense1 = tf.keras.layers.Dense(dv, activation='relu')
        self.dense2 = tf.keras.layers.Dense(dv)
        
    def split_heads(self, x, batch_size, dim):
        x = tf.reshape(x, (batch_size, -1, self.num_heads, dim))
        return tf.transpose(x, perm=[0, 2, 1, 3])
    
    def call(self, inputs):
        batch_size, time_steps, _ = tf.shape(inputs)
        
        q = self.conv_q(inputs)
        k = self.conv_k(inputs)
        v = self.dense_v(inputs)
        
        q = self.split_heads(q, batch_size, self.dk)
        k = self.split_heads(k, batch_size, self.dk)
        v = self.split_heads(v, batch_size, self.dv)
        
        mask = 1 - tf.linalg.band_part(tf.ones((batch_size, self.num_heads, time_steps, time_steps)), -1, 0)
        
        dk = tf.cast(self.dk, tf.float32)
        
        score = tf.nn.softmax(tf.matmul(q, k, transpose_b=True)/tf.math.sqrt(dk) + mask * -1e9)
        
        outputs = tf.matmul(score, v)
        
        outputs = tf.transpose(outputs, perm=[0, 2, 1, 3])
        outputs = tf.reshape(outputs, (batch_size, time_steps, -1))
        
        outputs = self.dense1(outputs)
        outputs = self.dense2(outputs)
        
        return outputs

class Transformer(tf.keras.models.Model):
    """
    Time Series Transformer Model
    """
    def __init__(self, dk, dv, num_heads, filter_size):
        super().__init__()
        # 注意，文章中使用了多层 Attention，为了简单起见，本 demo 只使用一层
        self.attention = Attention(dk, dv, num_heads, filter_size)
        self.dense_mu = tf.keras.layers.Dense(1)
        self.dense_sigma = tf.keras.layers.Dense(1, activation='softplus')
    
    def call(self, inputs):
        outputs = self.attention(inputs)
        mu = self.dense_mu(outputs)
        sigma = self.dense_sigma(outputs)
        
        return [mu, sigma]

关于损失函数和训练部分，请参考我们在介绍 DeepAR 时给出的 demo。

为了验证代码，我们随机生成一个带有周期的时间序列。下图展示了这个序列的一部分数据点。

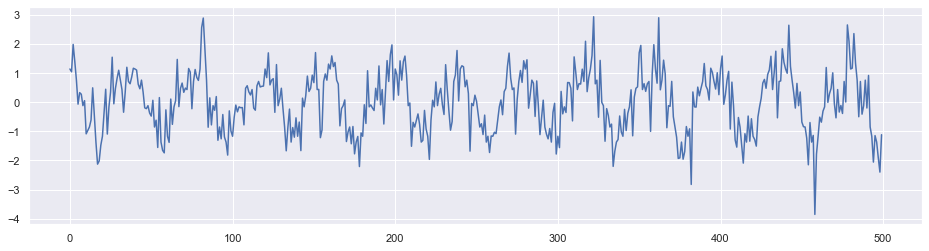
与 DeepAR 有所不同的是，由于 Attention 结构并不能很好地捕捉序列的顺序，我们加入了相对位置作为特征。

经过训练后用于预测，效果如下图所示，其中阴影部分表示 0.05 分位数 ~ 0.95 分位数的区间。

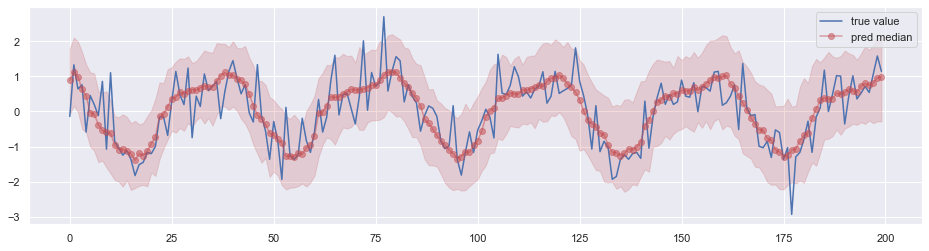
与 DeepAR 对比

从某种意义上来说，两者的网络结构很像，学习的也都是概率分布的参数。
Attention 结构本身不能很好地捕捉序列的顺序，当然这个不是大问题，因为通常来说时序预测任务都会有时间特征，不需要像自然语言处理时那样加入额外的位置编码。
该文章中给出的实验结果表明 Time Series Transformer 在捕捉长程依赖方面比 DeepAR 更有优势。
Time Series Transformer 在训练的时候可以并行计算，这是优于 DeepAR 的。不过因为和 DeepAR 一样采用了自回归结构，预测的时候无法并行。不仅如此，DeepAR 预测单个时间步时只需要使用当前输入和上一步输出的隐态即可；而 Transformer 却需要计算全局的 Attention。因此在预测的时候，Transformer 的计算效率很可能不如 DeepAR。

严格来说，该文章使用的并不是 Transformer。Google 的 Transformer 是一个 Encoder-Decoder 的结构，而该文章所使用的网络结构实际上是把 DeepAR 中的 LSTM 层替换为 Multi-Head Self Attention 层。这个结构其实一个（不完整的） Transformer Decoder 部分。But, whatever… ↩︎
原文没有这种说法。 ↩︎
这个图是我自己画的，原文没有。 ↩︎