前几天整理电脑的时候发现了本科上量子力学讨论班时做的一个 Slide,觉得挺有意思的。花了点时间整理成这篇博客。
一个质量为 m m m V ( x ) = 1 2 m ω 2 x 2 V(x) = \dfrac12m\omega^2x^2 V ( x ) = 2 1 m ω 2 x 2
H ^ = p ^ 2 2 m + 1 2 m ω 2 x ^ 2 \hat H = \frac{\hat p^2}{2m} + \frac12m\omega^2\hat x^2
H ^ = 2 m p ^ 2 + 2 1 m ω 2 x ^ 2
其中 x ^ \hat x x ^ p ^ = − i ℏ d d x \hat p = -i\hbar\dfrac{\mathrm d}{\mathrm dx} p ^ = − i ℏ d x d
H ^ ∣ ψ > = E ∣ ψ > \hat H\left|\psi\right> = E\left|\psi\right>
H ^ ∣ ψ ⟩ = E ∣ ψ ⟩
一维谐振子是除了氢原子之外,为数不多的可以解析求解的体系。那么我们为什么要费劲求它的数值解呢?正因为绝大多数的量子体系都无法解析求解,数值方法才显得尤为重要。
回忆一下泰勒公式
f ( a + h ) = f ( a ) + f ′ ( a ) 1 ! h + f ′ ′ ( a ) 2 ! h 2 + o ( h 3 ) f(a+h) = f(a) + \frac{f'(a)}{1!}h+\frac{f''(a)}{2!}h^2+o(h^3)
f ( a + h ) = f ( a ) + 1 ! f ′ ( a ) h + 2 ! f ′ ′ ( a ) h 2 + o ( h 3 )
令 h = − h h=-h h = − h
f ( a − h ) = f ( a ) − f ′ ( a ) 1 ! h + f ′ ′ ( a ) 2 ! h 2 + o ( h 3 ) f(a-h) = f(a) - \frac{f'(a)}{1!}h+\frac{f''(a)}{2!}h^2+o(h^3)
f ( a − h ) = f ( a ) − 1 ! f ′ ( a ) h + 2 ! f ′ ′ ( a ) h 2 + o ( h 3 )
两式相加,可得
f ′ ′ ( a ) = f ( a − h ) + f ( a + h ) − 2 f ( a ) h 2 + o ( h 3 ) ≈ f ( a − h ) + f ( a + h ) − 2 f ( a ) h 2 \begin{aligned}
f''(a) &= \frac{f(a-h)+f(a+h)-2f(a)}{h^2} + o(h^3)\\
&\approx \frac{f(a-h)+f(a+h)-2f(a)}{h^2}
\end{aligned}
f ′ ′ ( a ) = h 2 f ( a − h ) + f ( a + h ) − 2 f ( a ) + o ( h 3 ) ≈ h 2 f ( a − h ) + f ( a + h ) − 2 f ( a )
将 ψ ( x ) \psi(x) ψ ( x ) x ∈ [ − r , r ] x\in[-r, r] x ∈ [ − r , r ]
ϕ i ≡ ψ ( x i ) = ψ ( i Δ x − r ) , i = 0 , 1 , 2 , ⋯ , N \phi_i \equiv \psi(x_i) = \psi(i\Delta x - r),\quad i=0, 1, 2, \cdots, N
ϕ i ≡ ψ ( x i ) = ψ ( i Δ x − r ) , i = 0 , 1 , 2 , ⋯ , N
其中 N = 2 r / Δ x N=2r/\Delta x N = 2 r / Δ x
− ℏ 2 2 m ϕ i − 1 + ϕ i + 1 − 2 ϕ i Δ x 2 + 1 2 m ω 2 x i 2 ϕ i = E ϕ i -\frac{\hbar^2}{2m}\frac{\phi_{i-1}+\phi_{i+1}-2\phi_i}{\Delta x^2}+\frac12m\omega^2x_i^2\phi_i = E\phi_i
− 2 m ℏ 2 Δ x 2 ϕ i − 1 + ϕ i + 1 − 2 ϕ i + 2 1 m ω 2 x i 2 ϕ i = E ϕ i
在这里,我们假设 x < − r x<-r x < − r x > r x>r x > r ψ ( x ) → 0 \psi(x)\to 0 ψ ( x ) → 0
将差分方程写成矩阵的形式为
[ m ω 2 x 0 2 2 + ℏ 2 m Δ x 2 − ℏ 2 2 m Δ x 2 0 ⋯ 0 − ℏ 2 2 m Δ x 2 m ω 2 x 1 2 2 + ℏ 2 m Δ x 2 − ℏ 2 2 m Δ x 2 ⋯ 0 0 − ℏ 2 2 m Δ x 2 m ω 2 x 2 2 2 + ℏ 2 m Δ x 2 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ m ω 2 x N 2 2 + ℏ 2 m Δ x 2 ] [ ϕ 0 ϕ 1 ϕ 2 ⋮ ϕ N ] = E [ ϕ 0 ϕ 1 ϕ 2 ⋮ ϕ N ] \left[
\begin{matrix}
\frac{m\omega^2x_0^2}2+\frac{\hbar^2}{m\Delta x^2} & -\frac{\hbar^2}{2m\Delta x^2} & 0 & \cdots & 0\\
-\frac{\hbar^2}{2m\Delta x^2} & \frac{m\omega^2x_1^2}2+\frac{\hbar^2}{m\Delta x^2} & -\frac{\hbar^2}{2m\Delta x^2} & \cdots & 0\\
0 & -\frac{\hbar^2}{2m\Delta x^2} & \frac{m\omega^2x_2^2}2+\frac{\hbar^2}{m\Delta x^2} & \cdots & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \cdots & \frac{m\omega^2x_N^2}2+\frac{\hbar^2}{m\Delta x^2}
\end{matrix}
\right]
\left[
\begin{matrix}
\phi_0\\
\phi_1\\
\phi_2\\
\vdots\\
\phi_N
\end{matrix}
\right]= E
\left[
\begin{matrix}
\phi_0\\
\phi_1\\
\phi_2\\
\vdots\\
\phi_N
\end{matrix}
\right]
⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 2 m ω 2 x 0 2 + m Δ x 2 ℏ 2 − 2 m Δ x 2 ℏ 2 0 ⋮ 0 − 2 m Δ x 2 ℏ 2 2 m ω 2 x 1 2 + m Δ x 2 ℏ 2 − 2 m Δ x 2 ℏ 2 ⋮ 0 0 − 2 m Δ x 2 ℏ 2 2 m ω 2 x 2 2 + m Δ x 2 ℏ 2 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ 0 0 0 ⋮ 2 m ω 2 x N 2 + m Δ x 2 ℏ 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϕ 0 ϕ 1 ϕ 2 ⋮ ϕ N ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = E ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϕ 0 ϕ 1 ϕ 2 ⋮ ϕ N ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
这样一来,问题就转化为求差分矩阵的特征值和特征向量。
QR 算法是一种常见的特征值算法。它利用了矩阵的 QR 分解,即将矩阵 A A A Q Q Q R R R
A = Q R A=QR
A = Q R
为什么可以这么分解呢?我们回忆一下 Gram-Schmidt 正交化 ,将矩阵 A A A Q Q Q A A A A A A Q Q Q R R R Householder 变换 、Givens 旋转 等方法实现 QR 分解。
那么如何利用 QR 分解求解矩阵的特征值呢?
记 A 0 : = A A_0:=A A 0 : = A k = 0 , 1 , 2 , ⋯ k=0, 1, 2, \cdots k = 0 , 1 , 2 , ⋯
A k = Q k R k A k + 1 : = R k Q k \begin{aligned}
A_k &= Q_kR_k\\
A_{k+1} &:= R_kQ_k
\end{aligned}
A k A k + 1 = Q k R k : = R k Q k
即在每一步,对 A k A_k A k Q k Q_k Q k R k R_k R k A k + 1 A_{k+1} A k + 1
注意到 Q k Q_k Q k Q k − 1 = Q k ⊤ Q_k^{-1}=Q_k^\top Q k − 1 = Q k ⊤
A k + 1 = R k Q k = Q k − 1 Q k R k Q k = Q k − 1 A k Q k = Q k ⊤ A k Q k \begin{aligned}
A_{k+1} &= R_kQ_k\\
&= Q_k^{-1}Q_kR_kQ_k\\
&= Q_k^{-1}A_kQ_k\\
&= Q_k^\top A_kQ_k
\end{aligned}
A k + 1 = R k Q k = Q k − 1 Q k R k Q k = Q k − 1 A k Q k = Q k ⊤ A k Q k
也就是说,A k + 1 A_{k+1} A k + 1 A k A_k A k A 0 , A 1 , ⋯ , A k , ⋯ A_0, A_1, \cdots, A_k, \cdots A 0 , A 1 , ⋯ , A k , ⋯ A k A_k A k A k A_k A k
特别地,如果 A A A A k A_k A k Λ = d i a g { λ 0 , λ 1 , ⋯ , λ N } \Lambda=diag\{\lambda_0,\lambda_1,\cdots,\lambda_N\} Λ = d i a g { λ 0 , λ 1 , ⋯ , λ N } [ λ 0 , λ 1 , ⋯ , λ N ] [\lambda_0,\lambda_1,\cdots,\lambda_N] [ λ 0 , λ 1 , ⋯ , λ N ]
A = A 0 = Q 0 A 1 Q 0 ⊤ = ( Q 0 Q 1 ⋯ Q k − 1 ) A k ( Q k − 1 ⊤ ⋯ Q 1 ⊤ Q 0 ⊤ ) = ( Q 0 Q 1 ⋯ Q k − 1 ) A k ( Q 0 Q 1 ⋯ Q k − 1 ) ⊤ = S k A k S k ⊤ \begin{aligned}
A=A_0 &= Q_0A_1Q_0^\top\\
&=(Q_0Q_1\cdots Q_{k-1})A_k(Q_{k-1}^\top\cdots Q_1^\top Q_0^\top)\\
&=(Q_0Q_1\cdots Q_{k-1})A_k(Q_0Q_1\cdots Q_{k-1})^\top\\
&=S_kA_kS_k^\top
\end{aligned}
A = A 0 = Q 0 A 1 Q 0 ⊤ = ( Q 0 Q 1 ⋯ Q k − 1 ) A k ( Q k − 1 ⊤ ⋯ Q 1 ⊤ Q 0 ⊤ ) = ( Q 0 Q 1 ⋯ Q k − 1 ) A k ( Q 0 Q 1 ⋯ Q k − 1 ) ⊤ = S k A k S k ⊤
当 A k A_k A k S k S_k S k
综上,对于实对称正定矩阵 A A A A 0 = A , S 0 = I A_0=A, S_0=I A 0 = A , S 0 = I k = 0 , 1 , 2 , ⋯ k=0, 1, 2, \cdots k = 0 , 1 , 2 , ⋯
A k = Q k R k A k + 1 : = R k Q k S k + 1 : = S k Q k \begin{aligned}
A_k &= Q_kR_k\\
A_{k+1} &:= R_kQ_k\\
S_{k+1} &:= S_kQ_k
\end{aligned}
A k A k + 1 S k + 1 = Q k R k : = R k Q k : = S k Q k
当 A k A_k A k A A A
当年的我是一个彻头彻尾的门外汉,连调包都不会,QR 分解是用 C++ 手写的。然而那份如此有纪念意义的代码竟然被我弄丢了,真是痛惜不已。
如今的我已经误打误撞地成为了一名算法调包 工程师,知道可以直接调用 numpy.linalg.qr 作 QR 分解,可是却再也……再也想不出如何在这里编一段煽情的文字。
少废话,先看东西。
首先是 QR 算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 import numpy as npdef qr_eig (A, iters=200 , tol=1e-6 ): """ 使用 QR 算法求解实对称矩阵的特征值和特征向量 Parameters ---------- A : Array-like 二维数组,表示待求解的实对称矩阵 iters : int 最大迭代次数 tol : float 提前退出循环的判断标准 Returns ------- (numpy.ndarray, numpy.ndarray) 一维数组表示的特征值,二维数组表示的特征向量 """ A = np.asarray(A) S = np.eye(A.shape[0 ]) for _ in range (iters): Q, R = np.linalg.qr(A) newA = np.dot(R, Q) newS = np.dot(S, Q) if np.abs (max (np.diag(newA)) - max (np.diag(A))) < tol: break A = newA S = newS return np.diag(A), S
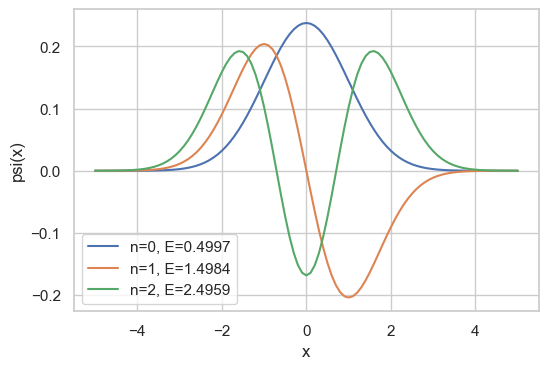
接下来就可以求解一维谐振子了。为了方便起见,我们令 ℏ = m = ω = 1 \hbar=m=\omega=1 ℏ = m = ω = 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 N = 101 r = 5 dx = 2 * r / (N - 1 ) x = np.linspace(-r, r, N, endpoint=True ) A = np.diag(0.5 *x**2 + 1 /dx**2 ) for i in range (N -1 ): A[i][i+1 ] = -0.5 /dx**2 A[i+1 ][i] = -0.5 /dx**2 Lambda, S = qr_eig(A) print(Lambda[-1 :-8 :-1 ]) plt.plot(x, S[:,-1 ], label=f'n=0, E={Lambda[-1 ]:.4 f} ' ) plt.plot(x, S[:,-2 ], label=f'n=1, E={Lambda[-2 ]:.4 f} ' ) plt.plot(x, S[:,-3 ], label=f'n=2, E={Lambda[-3 ]:.4 f} ' ) plt.xlabel('x' ) plt.ylabel('psi(x)' ) plt.legend()
1 >>> [0.4996873 1.49843574 2.49593067 3.49217016 4.48715598 ]
一维谐振子的本征能量为:
E n = ( n + 1 2 ) ℏ ω , n = 0 , 1 , 2 , ⋯ E_n = \left(n+\frac12\right)\hbar\omega,\qquad n=0, 1, 2,\cdots
E n = ( n + 2 1 ) ℏ ω , n = 0 , 1 , 2 , ⋯
对应的本征态为:
ψ n ( x ) = 1 2 n n ! ⋅ ( m ω π ℏ ) 1 / 4 ⋅ e − m ω x 2 / 2 ℏ ⋅ H n ( m ω ℏ x ) \psi_n(x) = \frac{1}{\sqrt{2^n n!}}\cdot\left(\frac{m\omega}{\pi\hbar}\right)^{1/4}\cdot\mathrm{e}^{-m\omega x^2/2\hbar}\cdot H_n\left(\sqrt{\frac{m\omega}{\hbar}}x\right)
ψ n ( x ) = 2 n n ! 1 ⋅ ( π ℏ m ω ) 1 / 4 ⋅ e − m ω x 2 / 2 ℏ ⋅ H n ( ℏ m ω x )
其中
H n ( z ) = ( − ) n e z 2 d n d z n ( e − z 2 ) H_n(z) = (-)^n\mathrm{e}^{z^2}\frac{\mathrm d^n}{\mathrm dz^n}\left(\mathrm{e}^{-z^2}\right)
H n ( z ) = ( − ) n e z 2 d z n d n ( e − z 2 )
为 Hermite 多项式。前三个 Hermite 多项式为:
H 0 ( z ) = 1 H 1 ( z ) = 2 z H 2 ( z ) = 4 z 2 − 2 \begin{aligned}
H_0(z) &= 1\\
H_1(z) &= 2z\\
H_2(z) &= 4z^2 - 2
\end{aligned}
H 0 ( z ) H 1 ( z ) H 2 ( z ) = 1 = 2 z = 4 z 2 − 2
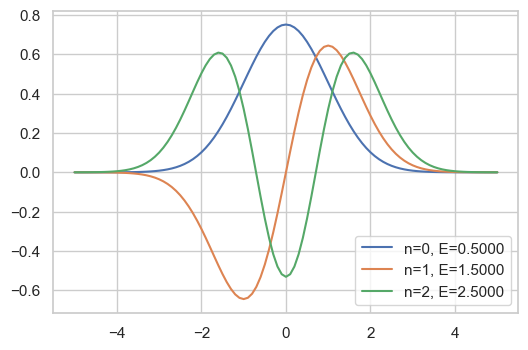
我们同样令 ℏ = m = ω = 1 \hbar=m=\omega=1 ℏ = m = ω = 1
E 0 = 1 2 , ψ 0 ( x ) = 1 π 1 / 4 ⋅ e − x 2 / 2 E 1 = 3 2 , ψ 1 ( x ) = 1 2 ⋅ 1 π 1 / 4 ⋅ e − x 2 / 2 ⋅ 2 x E 2 = 5 2 , ψ 2 ( x ) = 1 2 ⋅ 1 π 1 / 4 ⋅ e − x 2 / 2 ⋅ ( 2 x 2 − 1 ) \begin{aligned}
E_0&=\frac12, \qquad \psi_0(x) = \frac{1}{\pi^{1/4}}\cdot\mathrm{e}^{-x^2/2}\\
E_1&=\frac32, \qquad \psi_1(x) = \frac{1}{\sqrt 2}\cdot \frac{1}{\pi^{1/4}}\cdot\mathrm{e}^{-x^2/2}\cdot 2x\\
E_2&=\frac52, \qquad \psi_2(x) = \frac{1}{\sqrt 2}\cdot \frac{1}{\pi^{1/4}}\cdot\mathrm{e}^{-x^2/2}\cdot (2x^2-1)
\end{aligned}
E 0 E 1 E 2 = 2 1 , ψ 0 ( x ) = π 1 / 4 1 ⋅ e − x 2 / 2 = 2 3 , ψ 1 ( x ) = 2 1 ⋅ π 1 / 4 1 ⋅ e − x 2 / 2 ⋅ 2 x = 2 5 , ψ 2 ( x ) = 2 1 ⋅ π 1 / 4 1 ⋅ e − x 2 / 2 ⋅ ( 2 x 2 − 1 )
画出来看看
八九不离十吧。低能级的误差主要来自截断误差和舍入误差。此外,高能级需要有更大的 r r r x < − r x<-r x < − r x > r x>r x > r ψ ( x ) → 0 \psi(x)\to 0 ψ ( x ) → 0
Quantum harmonic oscillator - Wikipedia Finite difference method - Wikipedia QR algorithm - Wikipedia Notes on orthogonal bases and the workings of the QR algorithm QR decomposition - Wikipedia Gram–Schmidt process - Wikipedia