时间序列预测方法之 WaveNet

发表于 2019-11-08 更新于 2020-04-26 分类于调研分享阅读次数：

最近打算分享一些基于深度学习的时间序列预测方法。这是第四篇。

前面已经分享了两个基于 RNN 的模型（DeepAR 和 DeepState）和一个基于 Attention 的模型（Transformer），今次将会介绍一个基于 CNN 的模型。

Google DeepMind 在 2016 年发表了 WaveNet: A generative model for raw audio 。这篇文章介绍了一种用于音频生成的神经网络 WaveNet。该模型在文字转语音（Text-to-Speech, TTS）任务上取得了极佳的效果，与当时业界已有的模型不同，它合成的声音与真人的发音非常接近。目前 WaveNet 已经被应用在 Google Assistant 语音助手中。

WaveNet 是一个自回归概率模型，它将音波 $\mathrm x = \{x_1, \cdots, x_T\}$ 的联合概率分布建模为

p(\mathrm x) = \prod_{t=1}^Tp(x_t|x_1, \cdots, x_{t-1})

这种建模方式与 DeepAR 十分类似，因而可以很自然地迁移到时间序列预测的任务上——说起来音频信号本身也是一种时间序列。Amazon 在其开源的 GluonTS 库中就实现了一个基于 WaveNet 的时间序列预测模型。

接下来我会主要基于 DeepMind 的文章介绍一下 WaveNet 的网络结构，并给出一个 demo。

Model

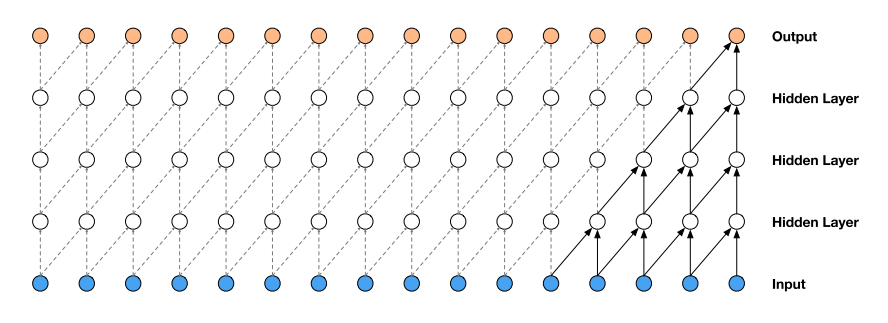
WaveNet 网络的基本单元是我们在介绍 Transformer 时提到过的因果卷积（causal convolution）。这种卷积方式可以确保模型在每一个时间步都不会接触到未来时间步的信息，如下图所示。

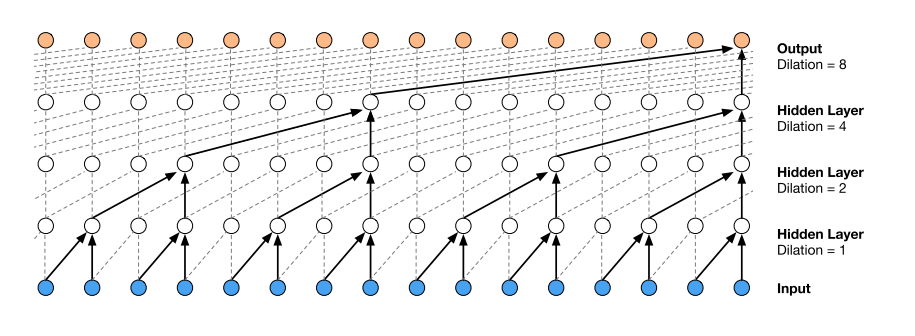
卷积的缺陷在于其本质上捕捉的是局部信息，需要通过增大卷积核或（和）增加模型层数的方式来扩大感受野。对于较长的序列，上述方法就杯水车薪了。为了解决这个问题，WaveNet 采用了空洞因果卷积（dilated causal convolution）。所谓空洞卷积，就是以一定的步长跳过输入值，将卷积核应用到超过其自身尺寸的区域，从而在层数不多的情况下也能拥有较大的感受野。如下图所示。

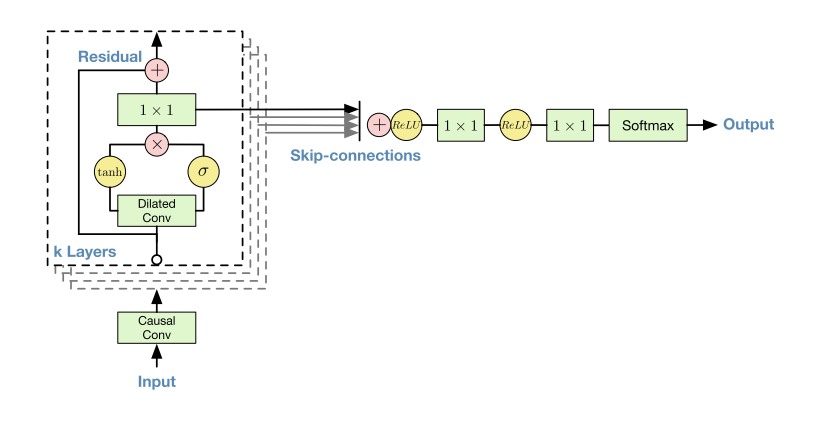
为了加快收敛以及训练更深的模型，WaveNet 使用了 residual connection 和 skip connection。完整的网络结构如下图所示。

注意到在残差块内部，使用了 gated activation unit 作为激活函数，即

output = \tanh(W_{f,k}* input) \odot \sigma(W_{g,k}* input)

文章声称在建模音频信号时这种激活函数的表现优于 ReLU。另一个有意思的细节是，WaveNet 在最后使用 Softmax 输出概率分布。Softmax 对分布的形状没有任何假设，文章认为这使得它适合用来拟合任意的分布。当然，这意味着需要将连续的数据离散化，并且训练时需要采用交叉熵作为损失函数。

Amazon 在进行时间序列预测时使用的网络结构与上述的内容并无二致，因而不需要再做过多介绍。预测时也是跟 DeepAR 一样的套路，先用自回归祖先采用获取一批样本，再利用样本计算感兴趣的统计量。这里比较有意思的是，在采样的时候，Amazon 给 Softmax 加了一个所谓的“温度” $T$ ，形如

p_i = \frac{\exp(z_i/T)}{\sum_j\exp(z_j/T)}

不难发现，“温度”越高，不同取值的概率越接近，得到的分布越平滑。这个做法十有八九是从知识蒸馏中借鉴过来的。

Code

Amazon 的实现是基于 MXNet 的。我们还是延续之前的做法，自己用 TensorFlow 构建一个 demo。

下面给出残差块和网络结构的定义：

import tensorflow as tf

class DilatedCausalResidual(tf.keras.layers.Layer):
    """
    空洞因果卷积残差块
    """
    def __init__(self, dilation_rate, kernel_size, residual_channels, dilation_channels, skip_channels, return_dense):
        super().__init__()
        self.return_dense = return_dense
        
        self.conv_tanh = tf.keras.layers.Conv1D(
            filters=dilation_channels,
            kernel_size=kernel_size,
            strides=1,
            padding='causal',
            dilation_rate=dilation_rate,
            activation='tanh'
        )
        self.conv_sigmoid = tf.keras.layers.Conv1D(
            filters=dilation_channels,
            kernel_size=kernel_size,
            strides=1,
            padding='causal',
            dilation_rate=dilation_rate,
            activation='sigmoid'
        )
        self.conv_skip = tf.keras.layers.Conv1D(
            filters=skip_channels,
            kernel_size=1,
            strides=1,
            padding='causal'
        )
        if self.return_dense:
            self.conv_residual = tf.keras.layers.Conv1D(
                filters=residual_channels,
                kernel_size=1,
                strides=1,
                padding='causal'
            )
        else:
            self.conv_residual = None
    
    
    def call(self, inputs):
        tanh = self.conv_tanh(inputs)
        sigmoid = self.conv_sigmoid(inputs)
        
        z = tf.multiply(tanh, sigmoid)
        skip = self.conv_skip(z)
        
        if not self.return_dense:
            return skip, None
        
        residual = self.conv_residual(z)
        dense = inputs + residual
        
        return skip, dense


class WaveNet(tf.keras.models.Model):
    """
    WaveNet 模型
    """
    def __init__(self, dilation_rates, kernel_size, residual_channels, dilation_channels, skip_channels, logits_channels):
        super().__init__()
        
        self.causal_conv = tf.keras.layers.Conv1D(
            filters=residual_channels,
            kernel_size=kernel_size,
            strides=1,
            padding='causal'
        )
        
        self.residual_stacks = []
        for i, dilation_rate in enumerate(dilation_rates):
            is_not_last = i < len(dilation_rates) - 1
            self.residual_stacks.append(
                DilatedCausalResidual(
                    dilation_rate=dilation_rate,
                    kernel_size=kernel_size,
                    residual_channels=residual_channels,
                    dilation_channels=dilation_channels,
                    skip_channels=skip_channels,
                    return_dense=is_not_last
                )
            )
        
        self.relu = tf.keras.layers.Activation('relu')
        self.conv1 = tf.keras.layers.Conv1D(
            filters=skip_channels,
            kernel_size=1,
            strides=1
        )
        self.conv2 = tf.keras.layers.Conv1D(
            filters=logits_channels,
            kernel_size=1,
            strides=1
        )
        
    def call(self, inputs):
        o = self.causal_conv(inputs)
        
        skip_outs = []
        for block in self.residual_stacks:
            skip, o = block(o)
            skip_outs.append(skip)
        
        total = sum(skip_outs)
        outputs = self.relu(total)
        outputs = self.conv1(outputs)
        outputs = self.relu(outputs)
        outputs = self.conv2(outputs)
        
        # 这里直接输出 logits
        return outputs

训练过程与之前介绍的模型大同小异，这里不再赘述了。

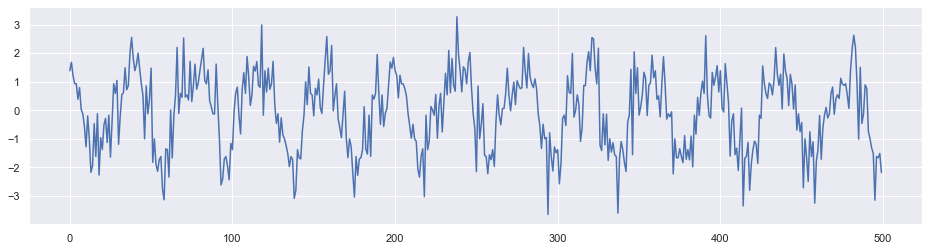
为了验证代码，我们随机生成一个带有周期的时间序列。下图展示了这个序列的一部分数据点。

简单起见，我们没有加入额外的特征。

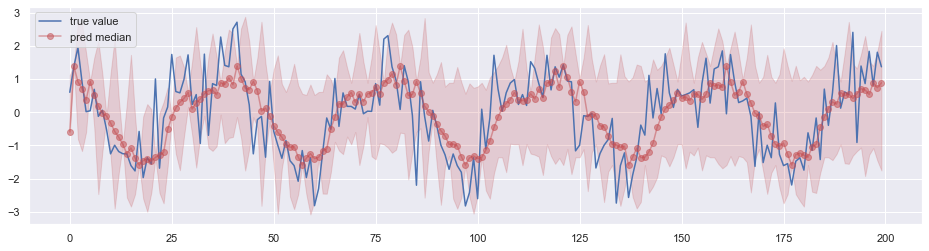
经过训练后用于预测，效果如下图所示，其中阴影部分表示 0.05 分位数 ~ 0.95 分位数的区间。

与其它模型对比

WaveNet 与之前介绍的 DeepAR 和 Transformer 类似，都是自回归模型。
DeepAR 基于 RNN，在训练的时候无法并行。Transformer 基于 Attention，WaveNet 基于 CNN，它们训练时都是并行的。
自回归模型在预测时都无法并行。但 DeepAR 的 RNN 结构保留了网络状态，采样时的计算量最小。Transformer 每采样一个时间步都需要进行一次全局 Self Attention，计算量最大。从 Amazon 给出的实现中可以看到，WaveNet 在经过适当改造之后，能够利用缓存减少不必要的重复计算，从而加速采样。
DeepAR 和 Transformer 学习的是概率分布的参数，WaveNet 学习的是 Softmax 的 logits。由于前两者假定了分布的形状，因而预测的结果看上去较为规则。将 WaveNet 的学习目标改为与前两者一样似乎也未尝不可，不过效果如何需要通过实验来验证。