卡尔曼滤波简介

发表于 更新于 分类于

最近学习了一种结合了深度学习和状态空间模型的时间序列预测方法（见《时间序列预测方法之 DeepState》），该方法需要用到卡尔曼滤波。

卡尔曼滤波是一种高效的自回归滤波器，它能够从一系列不完全及包含噪声的测量中，估计动态系统的状态。在导航、运动控制、时间序列分析等领域都有重要应用。

卡尔曼滤波的公式比较多，乍一看容易懵。根据我多年的经验，遇到让人头疼的公式，自己试着推导一遍，肯定会更头疼， 比较有助于理解。

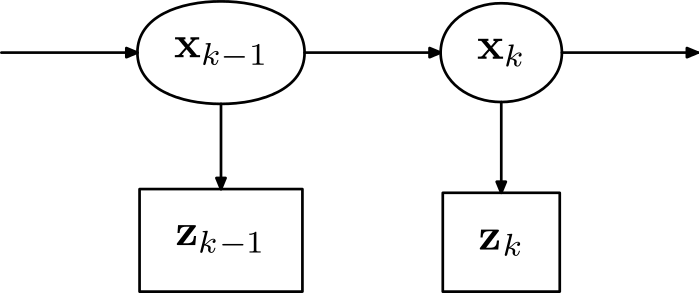
先简单介绍一下状态空间模型。如下图所示。系统的状态 {xk}\{x_k\}构成一条马尔科夫链。我们无法直接观测状态 xkx_k，而是通过可观测的量 zkz_k 来估计当前的状态。

考虑一个线性高斯状态空间模型，有

  • 状态转移方程：

xk=Fkxk−1+Bkuk+wk(1)x_k = F_kx_{k-1} + B_ku_k + w_k \tag 1

其中 xkx_k 表示 kk 时刻系统的状态，FkF_k 是状态转移模型，uku_k 表示 kk 时刻系统的输入，BkB_k 是输入控制模型，wkw_k 是状态转移时的噪声，满足 wk∼N(0,Qk)w_k\sim N(0, Q_k)。

  • 观测方程：

zk=Hkxk+vk(2)z_k = H_kx_k + v_k \tag 2

其中 zkz_k 是 kk 时刻的观测值，HkH_k 是观测模型亦即从真实状态空间到观测空间的映射，vkv_k 是观测时的噪声，满足 vk∼N(0,Rk)v_k\sim N(0, R_k)。

在已知 k−1k-1 个观测值的情况下，我们可以估计 kk 时刻的状态：

x^k∣k−1=Fkx^k−1∣k−1+Bkuk(3)\hat{x}_{k|k-1} = F_k\hat{x}_{k-1|k-1} + B_ku_k \tag 3

在得到第 kk 个观测值后，计算观测值与估计的观测值之间的偏差：

y~k=zk−Hkx^k∣k−1(4)\tilde{y}_k = z_k - H_k\hat{x}_{k|k-1} \tag 4

从而可以对估计的状态作出修正：

x^k∣k=x^k∣k−1+Kky~k(5)\hat{x}_{k|k} = \hat{x}_{k|k-1} + K_k\tilde{y}_k \tag 5

这很明显是一个贝叶斯主义者的做法：你先有个信念（估计），在得到新的证据（观测值）后，以一定的权重更新你的信念。

这里的权重 KkK_k 被称为增益。接下来我们来推导最优的增益。先考虑以下几个协方差：

Pk∣k=cov(xk−x^k∣k)Pk∣k−1=cov(xk−x^k∣k−1)Sk=cov(y~k)(6)\begin{aligned} P_{k|k} &= \mathrm{cov}(x_k - \hat{x}_{k|k})\\ P_{k|k-1} &= \mathrm{cov}(x_k - \hat{x}_{k|k-1})\\ S_k &= \mathrm{cov}( \tilde{y}_k) \end{aligned} \tag 6

在接下来的推导中，我会尽可能给出完整的中间步骤。

Sk=cov(y~k)=cov(zk−Hkx^k∣k−1)=cov(Hkxk+vk−Hkx^k∣k−1)=cov(Hk(xk−x^k∣k−1)+vk)=Hkcov(xk−x^k∣k−1)Hk⊤+cov(vk)=HkPk∣k−1Hk⊤+Rk(7)\begin{aligned} S_k &= \mathrm{cov}(\tilde{y}_k)\\ &= \mathrm{cov}( z_k - H_k\hat{x}_{k|k-1})\\ &= \mathrm{cov}(H_kx_k + v_k - H_k\hat{x}_{k|k-1})\\ &=\mathrm{cov}(H_k(x_k - \hat{x}_{k|k-1}) + v_k)\\ &= H_k\mathrm{cov}(x_k - \hat{x}_{k|k-1})H_k^\top + \mathrm{cov}(v_k)\\ &= H_kP_{k|k-1}H_k^\top + R_k \end{aligned} \tag 7

Pk∣k−1=cov(xk−x^k∣k−1)=cov(Fkxk−1+Bkuk+wk−(Fkx^k−1∣k−1+Bkuk))=cov(Fk(xk−1−x^k−1∣k−1)+wk)=Fkcov(xk−1−x^k−1∣k−1)Fk⊤+cov(wk)=FkPk−1∣k−1Fk⊤+Qk(8)\begin{aligned} P_{k|k-1} &= \mathrm{cov}(x_k - \hat{x}_{k|k-1})\\ &= \mathrm{cov}(F_kx_{k-1} + B_ku_k + w_k - (F_k\hat{x}_{k-1|k-1} + B_ku_k))\\ &= \mathrm{cov}(F_k(x_{k-1}-\hat{x}_{k-1|k-1}) + w_k)\\ &= F_k\mathrm{cov}(x_{k-1}-\hat{x}_{k-1|k-1})F_k^\top + \mathrm{cov}(w_k)\\ &= F_kP_{k-1|k-1}F_k^\top + Q_k\\ \end{aligned} \tag 8

而

Pk∣k=cov(xk−x^k∣k)=cov(xk−x^k∣k−1−Kky~k)=cov(xk−x^k∣k−1−Kk(zk−Hkx^k∣k−1))=cov(xk−x^k∣k−1−Kk(Hkxk+vk−Hkx^k∣k−1))=cov((I−KkHk)(xk−x^k∣k−1)−Kkvk)=(I−KkHk)cov(xk−x^k∣k−1)(I−KkHk)⊤+Kkcov(vk)Kk⊤=(I−KkHk)Pk∣k−1(I−KkHk)⊤+KkRkKk⊤=Pk∣k−1−KkHkPk∣k−1−Pk∣k−1Hk⊤Kk⊤+KkHkPk∣k−1Hk⊤Kk⊤+KkRkKk⊤=Pk∣k−1−KkHkPk∣k−1−Pk∣k−1Hk⊤Kk⊤+Kk(HkPk∣k−1HkT+Rk)Kk⊤=Pk∣k−1−KkHkPk∣k−1−Pk∣k−1Hk⊤Kk⊤+KkSkKk⊤(9)\begin{aligned} P_{k|k} &= \mathrm{cov}(x_k - \hat{x}_{k|k})\\ &= \mathrm{cov}(x_k - \hat{x}_{k|k-1} - K_k\tilde{y}_k)\\ &= \mathrm{cov}(x_k - \hat{x}_{k|k-1} - K_k(z_k - H_k\hat{x}_{k|k-1}))\\ &= \mathrm{cov}(x_k - \hat{x}_{k|k-1} - K_k(H_kx_k + v_k - H_k\hat{x}_{k|k-1}))\\ &= \mathrm{cov}((I-K_k H_k)(x_k - \hat{x}_{k|k-1}) - K_k v_k)\\ &= (I-K_kH_k)\mathrm{cov}(x_k - \hat{x}_{k|k-1})(I-K_k H_k)^\top + K_k\mathrm{cov}(v_k)K_k^\top\\ &= (I-K_kH_k)P_{k|k-1}(I-K_kH_k)^\top + K_kR_kK_k^\top\\ &= P_{k|k-1} - K_kH_kP_{k|k-1} - P_{k|k-1}H_k^\top K_k^\top + K_kH_kP_{k|k-1}H_k^\top K_k^\top + K_kR_kK_k^\top\\ &= P_{k|k-1} - K_kH_kP_{k|k-1} - P_{k|k-1}H_k^\top K_k^\top + K_k(H_kP_{k|k-1}H_k^T + R_k)K_k^\top\\ &= P_{k|k-1} - K_kH_kP_{k|k-1} - P_{k|k-1}H_k^\top K_k^\top + K_kS_kK_k^\top \end{aligned} \tag 9

优化的目标是最小化均方误差，即最小化 E[∣xk−x^k∣k∣2]=tr(Pk∣k)\mathbb{E}[|x_k - \hat{x}_{k|k}|^2] = \mathrm{tr}(P_{k|k})。令

∂tr(Pk∣k)∂Kk=0=∂∂Kktr(Pk∣k−1−KkHkPk∣k−1−Pk∣k−1Hk⊤Kk⊤+KkSkKk⊤)=∂∂Kk[−tr(KkHkPk∣k−1)−tr(Pk∣k−1Hk⊤Kk⊤)+tr(KkSkKk⊤)]=∂∂Kk[−tr(KkHkPk∣k−1)−tr(Pk∣k−1(KkHk)⊤)+tr(KkSkKk⊤)]=∂∂Kk[−tr(KkHkPk∣k−1)−tr((KkHkPk∣k−1top)⊤)+tr(KkSkKk⊤)]=∂∂Kk[−tr(KkHkPk∣k−1)−tr((KkHkPk∣k−1)⊤)+tr(KkSkKk⊤)]=∂∂Kk[−tr(KkHkPk∣k−1)−tr(KkHkPk∣k−1)+tr(KkSkKk⊤)]=∂∂Kk[−2tr(KkHkPk∣k−1)+tr(KkSkKk⊤)]=−2(HkPk∣k−1)⊤+KkSk+KkSk⊤=−2(HkPk∣k−1)⊤+2KkSk(10)\begin{aligned} \frac{ \partial \mathrm{tr}(P_{k|k})}{ \partial K_k} &= 0\\ &= \frac{\partial }{\partial K_k}\mathrm{tr}(P_{k|k-1} - K_kH_kP_{k|k-1} - P_{k|k-1}H_k^\top K_k^\top + K_k S_k K_k^\top)\\ &= \frac{\partial }{\partial K_k}[- \mathrm{tr}(K_kH_kP_{k|k-1}) - \mathrm{tr}(P_{k|k-1}H_k^\top K_k^\top) + \mathrm{tr}(K_kS_kK_k^\top)]\\ &= \frac{\partial }{\partial K_k}[- \mathrm{tr}(K_kH_kP_{k|k-1}) - \mathrm{tr}(P_{k|k-1}(K_kH_k)^\top) + \mathrm{tr}(K_kS_kK_k^\top)]\\ &= \frac{\partial }{\partial K_k}[ - \mathrm{tr}(K_kH_kP_{k|k-1}) - \mathrm{tr}((K_kH_kP_{k|k-1}^ top)^\top) + \mathrm{tr}(K_kS_kK_k^\top)]\\ &= \frac{\partial }{\partial K_k}[ - \mathrm{tr}(K_kH_kP_{k|k-1}) - \mathrm{tr}((K_kH_kP_{k|k-1})^\top) + \mathrm{tr}(K_kS_kK_k^\top)]\\ &= \frac{\partial }{\partial K_k}[ - \mathrm{tr}(K_kH_kP_{k|k-1}) - \mathrm{tr}(K_kH_kP_{k|k-1}) + \mathrm{tr}(K_kS_kK_k^\top)]\\ &= \frac{\partial }{\partial K_k}[ - 2\mathrm{tr}(K_kH_kP_{k|k-1}) + \mathrm{tr}(K_kS_kK_k^\top)]\\ &= -2(H_kP_{k|k-1})^\top + K_kS_k + K_kS_k^\top\\ &= -2(H_kP_{k|k-1})^\top + 2K_kS_k \end{aligned} \tag{10}

解得最优卡尔曼增益

Kk=(HkPk∣k−1)⊤Sk−1=Pk∣k−1Hk⊤Sk−1(11)K_k = (H_kP_{k|k-1})^\top S_k^{-1} = P_{k|k-1}H_k^\top S_k^{-1} \tag{11}

此时式 (9) 可以进一步简化为

Pk∣k=Pk∣k−1−KkHkPk∣k−1−Pk∣k−1Hk⊤Kk⊤+KkSkKk⊤=Pk∣k−1−KkHkPk∣k−1−Pk∣k−1Hk⊤Kk⊤+Pk∣k−1Hk⊤Sk−1SkKk⊤=Pk∣k−1−KkHkPk∣k−1−Pk∣k−1Hk⊤Kk⊤+Pk∣k−1Hk⊤Kk⊤=Pk∣k−1−KkHkPk∣k−1(12)\begin{aligned} P_{k|k} &= P_{k|k-1} - K_kH_kP_{k|k-1} - P_{k|k-1}H_k^\top K_k^\top + K_kS_kK_k^\top\\ &= P_{k|k-1} - K_kH_kP_{k|k-1} - P_{k|k-1}H_k^\top K_k^\top + P_{k|k-1}H_k^\top S_k^{-1}S_kK_k^\top\\ &= P_{k|k-1} - K_kH_kP_{k|k-1} - P_{k|k-1}H_k^\top K_k^\top + P_{k|k-1}H_k^\top K_k^\top\\ &= P_{k|k-1} - K_kH_kP_{k|k-1} \end{aligned} \tag{12}

推导到这里，基本上也就彻底糊涂一目了然了。接下来看看这些公式怎么用。

卡尔曼滤波器的操作包括两个阶段：预测与更新。在预测阶段，滤波器使用上一状态的估计，做出对当前状态的估计。在更新阶段，滤波器利用对当前状态的观测值优化在预测阶段获得的预测值，以获得一个更精确的新估计值。

在预测阶段，用式 (3) 和式 (8) 给出预测状态和预测估计协方差矩阵：

x^k∣k−1=Fkx^k−1∣k−1+BkukPk∣k−1=FkPk−1∣k−1Fk⊤+Qk\begin{aligned} \hat{x}_{k|k-1} &= F_k\hat{x}_{k-1|k-1} + B_ku_k\\ P_{k|k-1} &= F_kP_{k-1|k-1}F_k^\top + Q_k\\ \end{aligned}

在更新阶段，先用式 (4)、式 (7) 和式 (11) 分别计算测量余量、测量余量的协方差和最优卡尔曼增益：

y~k=zk−Hkx^k∣k−1Sk=HkPk∣k−1Hk⊤+RkKk=Pk∣k−1Hk⊤Sk−1\begin{aligned} \tilde{y}_k &= z_k - H_k\hat{x}_{k|k-1}\\ S_k &= H_kP_{k|k-1}H_k^\top + R_k\\ K_k & = P_{k|k-1}H_k^\top S_k^{-1} \end{aligned}

再用式 (5) 和式 (12) 分别计算更新后的状态估计和协方差估计：

x^k∣k=x^k∣k−1+Kky~kPk∣k=Pk∣k−1−KkHkPk∣k−1\begin{aligned} \hat{x}_{k|k} &= \hat{x}_{k|k-1} + K_k\tilde{y}_k\\ P_{k|k} &= P_{k|k-1} - K_kH_kP_{k|k-1} \end{aligned}

只要知道初始时刻的 x^0∣0\hat{x}_{0|0} 和 P0∣0P_{0|0} 就可以递归地计算 x^k∣k\hat{x}_{k|k} 和 Pk∣kP_{k|k} 了（完