时间序列中的异常

发表于 2018-11-27 更新于 2020-04-01 分类于调研分享阅读次数：

考虑一个 ARIMA 过程生成的时间序列

Y_t = \frac{\theta(B)}{\alpha(B)\phi(B)}a_t, \qquad t = 1, 2, \cdots, n

其中 $\theta(B)$ 和 $\phi(B)$ 的所有根都在单位圆外， $\alpha(B)$ 的所有根都在单位圆上。

在这个序列中引入一个异常，得到

Y_t^* = Y_t + \omega\frac{A(B)}{G(B)H(B)}I_t(\tau)

其中

I_t(\tau) = \begin{cases} 1, & t= \tau,\\ 0, & otherwise \end{cases}

$\tau$ 表示异常发生的时刻， $\omega$ 表示异常的量级， $\frac{A(B)}{G(B)H(B)}$ 表示异常的演化模式。

下面考虑 4 种特定的异常，分别是 innovational outlier (IO)，additive outlier (AO)，level shift (LS) 以及 temporary change (TC)。它们的定义如下：

\begin{aligned} IO:\qquad \frac{A(B)}{G(B)H(B)} &= \frac{\theta(B)}{\alpha(B)\phi(B)},\\ AO:\qquad \frac{A(B)}{G(B)H(B)} &= 1, \\ TC:\qquad \frac{A(B)}{G(B)H(B)} &= \frac 1{1-\delta B}, \qquad (0<\delta<1),\\ LS:\qquad \frac{A(B)}{G(B)H(B)} &= \frac 1{1-B}. \end{aligned}

additive outlier (AO) 表现为序列的值在单次观测中突然变大或变小，而随后的观察结果不受异常值的影响。level shift (LS) 在异常值之后出现的所有观察值都偏移到一个新的水平。temporary change (TC) 和 LS 类似，只不过异常值的影响在随后的观察中呈指数减小，序列最终会回归到正常水平。实际上 AO 和 LS 可以看作是 TC 在 $\delta=0$ 和 $\delta=1$ 时的特例。这 3 种异常和系统之间是独立的，而 innovational outlier (IO) 则不然。IO 通过时间序列的相关结构，波及到与之邻近的一系列观察点。

例子：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from scipy.signal import lfilter, unit_impulse

def arma_process(ar, ma, size=200, scale=1., e=None):
    if e is None:
        e = np.random.normal(size=size)
    return lfilter(ma, ar, scale*e)

# 考虑一个 ARMA(1, 1) 模型
ar = [1, 0.85]
ma = [1, 0.65]

sample = arma_process(ar, ma)
io = arma_process(ar, ma, e=10*unit_impulse(200, 100))
ao = 10*unit_impulse(200, 100)
tc = arma_process([1, -0.9], [1], e=10*unit_impulse(200, 100))
ls = arma_process([1, -1], [1], e=10*unit_impulse(200, 100))

x = range(200)
plt.figure(figsize=(12, 12))
plt.subplot(511)
plt.plot(x, sample)
plt.title('original signal')

plt.subplot(523)
plt.plot(x, io)
plt.title('innovational outlier (IO)')
plt.subplot(524)
plt.plot(x, sample+io, label='with IO')
plt.plot(x, sample, label='without IO')
plt.title('signal with IO')
plt.legend()

plt.subplot(525)
plt.plot(x, ao)
plt.title('additive outlier (AO)')
plt.subplot(526)
plt.plot(x, sample+ao, label='with AO')
plt.plot(x, sample, label='without AO')
plt.title('signal with AO')
plt.legend()

plt.subplot(527)
plt.plot(x, tc)
plt.title('temporary change (TC)')
plt.subplot(528)
plt.plot(x, sample+tc, label='with TC')
plt.plot(x, sample, label='without TC')
plt.title('signal with TC')
plt.legend()

plt.subplot(529)
plt.plot(x, ls)
plt.title('level shift (LS)')
plt.subplot(5,2,10)
plt.plot(x, sample+ls, label='with LS')
plt.plot(x, sample, label='without LS')
plt.title('signal with LS')
plt.legend()

plt.tight_layout()
plt.show()

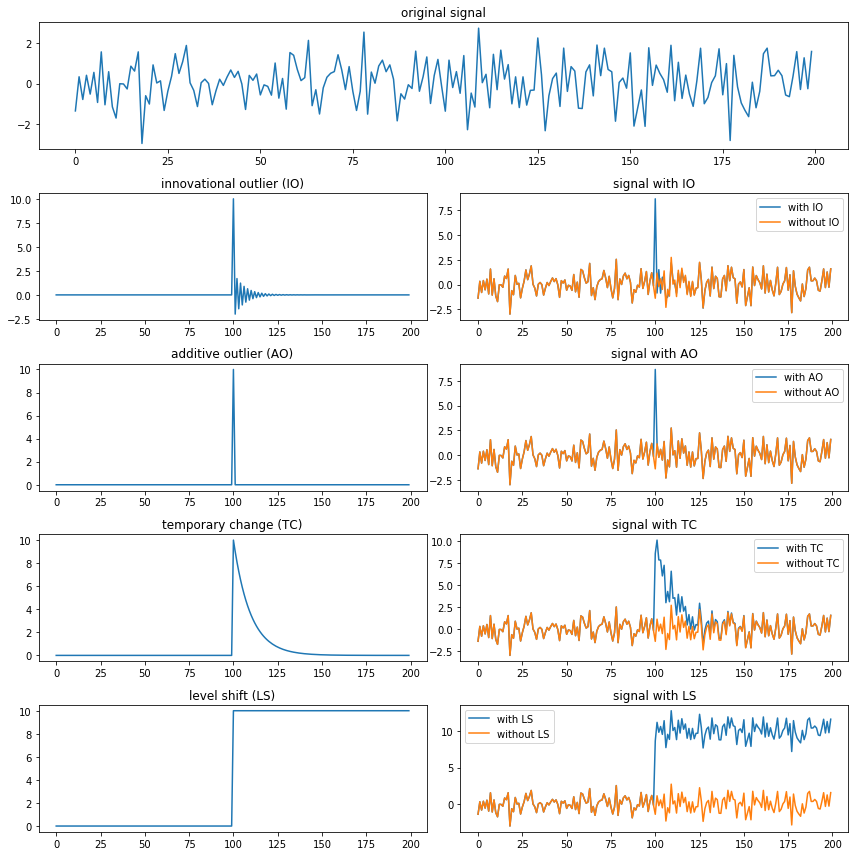
更复杂的异常通常可以近似看作这几种异常的组合。

在 $\tau_1, \tau_2, \cdots, \tau_m$ 引入 m 个异常，则时间序列可以表示为：

Y_t^* = Y_t + \sum\limits_{j=1}^m\omega_jL_j(B)I_t(\tau_j)

其中 $L_j(B)$ 为 $t_j$ 处异常的演化模式。

算命笔记

时间序列中的异常

参考文献