指数平滑方法简介

发表于 更新于 分类于

指数平滑（Exponential smoothing）是除了 ARIMA 之外的另一种被广泛使用的时间序列预测方法（关于 ARIMA，请参考 时间序列模型简介）。 指数平滑即指数移动平均（exponential moving average），是以指数式递减加权的移动平均。各数值的权重随时间指数式递减，越近期的数据权重越高。常用的指数平滑方法有一次指数平滑、二次指数平滑和三次指数平滑。

1. 一次指数平滑

一次指数平滑又叫简单指数平滑（simple exponential smoothing， SES），适合用来预测没有明显趋势和季节性的时间序列。其预测结果是一条水平的直线。模型形如：

Forecast equation: y^t+h∣t=lt\hat{y}_{t+h|t} = l_t
Smoothing equantion: lt=αyt+(1−α)lt−1l_t = \alpha y_t + (1-\alpha)l_{t-1}

其中 yty_t 是真实值，y^t+h(h∈Z+)\hat{y}_{t+h} (h\in Z^+) 为预测值，ltl_t 为平滑值， 0<α<10< \alpha < 1。

定义残差 ϵt=yt−y^t∣t−1\epsilon_t = y_t - \hat{y}_{t|t-1}，其中 t=1,⋯ ,Tt=1,\cdots,T，则可以通过优化方法得到 α\alpha 和 l0l_0。

(α∗,l0∗)=min⁡(α,l0)∑t=1Tϵt2=min⁡(α,l0)∑t=1T(yt−y^t∣t−1)2(\alpha^*, l_0^*) = \min\limits_{(\alpha, l_0)}\sum\limits_{t=1}^T\epsilon_t^2 = \min\limits_{(\alpha, l_0)}\sum\limits_{t=1}^T\left(y_t - \hat{y}_{t|t-1}\right)^2

使用 python 的 statsmodels 可以方便地应用该模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import SimpleExpSmoothing

x1 = np.linspace(0, 1, 100)
y1 = pd.Series(np.multiply(x1, (x1 - 0.5)) + np.random.randn(100))
ets1 = SimpleExpSmoothing(y1)
r1 = ets1.fit()
pred1 = r1.predict(start=len(y1), end=len(y1) + len(y1)//2)

pd.DataFrame({
    'origin': y1,
    'fitted': r1.fittedvalues,
    'pred': pred1
}).plot(legend=True)

效果如图：

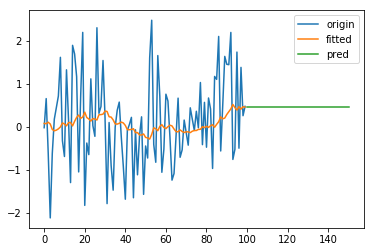
2. 二次指数平滑

2.1 Holt’s linear trend method

Holt 扩展了简单指数平滑，使其可以用来预测带有趋势的时间序列。直观地看，就是对平滑值的一阶差分（可以理解为斜率）也作一次平滑。模型的预测结果是一条斜率不为0的直线。模型形如：

Forecast equation: y^t+h∣t=lt+hbt\hat{y}_{t+h|t} = l_t + hb_t
Level equation: lt=αyt+(1−α)(lt−1+bt−1)l_t = \alpha y_t + (1-\alpha)(l_{t-1} + b_{t-1})
Trend equation: bt=β(lt−lt−1)+(1−β)bt−1b_t = \beta(l_t - l_{t-1}) + (1-\beta)b_{t-1}

其中 0<α<10< \alpha < 1， 0<β<10< \beta < 1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from statsmodels.tsa.holtwinters import Holt

x2 = np.linspace(0, 99, 100)
y2 = pd.Series(0.1 * x2 + 2 * np.random.randn(100))
ets2 = Holt(y2)
r2 = ets2.fit()
pred2 = r2.predict(start=len(y2), end=len(y2) + len(y2)//2)

pd.DataFrame({
    'origin': y2,
    'fitted': r2.fittedvalues,
    'pred': pred2
}).plot(legend=True)

效果如图：

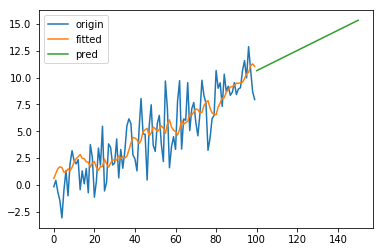
2.2 Damped trend methods

Holt’s linear trend method 得到的预测结果是一条直线，即认为未来的趋势是固定的。对于短期有趋势、长期趋于稳定的序列，可以引入一个阻尼系数 0<ϕ<10<\phi<1，将模型改写为

Forecast equation: y^t+h∣t=lt+(ϕ+ϕ2+⋯+ϕh)bt\hat{y}_{t+h|t} = l_t + (\phi + \phi^2 + \cdots +\phi^h)b_t
Level equation: lt=αyt+(1−α)(lt−1+ϕbt−1)l_t = \alpha y_t + (1-\alpha)(l_{t-1} + \phi b_{t-1})
Trend equation: bt=β(lt−lt−1)+(1−β)ϕbt−1b_t = \beta(l_t - l_{t-1}) + (1-\beta)\phi b_{t-1}

3. 三次指数平滑

为了描述时间序列的季节性，Holt 和 Winters 进一步扩展了 Holt’s linear trend method，得到了三次指数平滑模型，也就是通常说的 Holt-Winters’ 模型。我们用 mm 表示“季节”的周期。根据季节部分和非季节部分的组合方式不同，Holt-Winters’ 又可以分为加法模型和乘法模型。

3.1 Holt-Winters’ additive method

加法模型形如：

Forecast equation: y^t+h∣t=lt+hbt+st+h−m(k+1)\hat{y}_{t+h|t} = l_t + hb_t + s_{t+h-m(k+1)}
Level equation: lt=α(yt−st−m)+(1−α)(lt−1+bt−1)l_t = \alpha(y_t - s_{t-m}) + (1-\alpha)(l_{t-1} + b_{t-1})
Trend equation: bt=β(lt−lt−1)+(1−β)bt−1b_t = \beta(l_t - l_{t-1}) + (1-\beta)b_{t-1}
Seasonal equation: st=γ(yt−lt−1−bt−1)+(1−γ)st−ms_t = \gamma(y_t - l_{t-1} - b_{t-1}) + (1-\gamma)s_{t-m}

其中 0<α<10< \alpha < 1， 0<β<10< \beta < 1，0<γ<10< \gamma < 1。kk 是 h−1m\dfrac{h-1}m 的整数部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from statsmodels.tsa.holtwinters import ExponentialSmoothing

x3 = np.linspace(0, 4 * np.pi, 100)
y3 = pd.Series(20 + 0.1 * np.multiply(x3, x3) + 8 * np.cos(2 * x3) + 2 * np.random.randn(100))
ets3 = ExponentialSmoothing(y3, trend='add', seasonal='add', seasonal_periods=25)
r3 = ets3.fit()
pred3 = r3.predict(start=len(y3), end=len(y3) + len(y3)//2)

pd.DataFrame({
    'origin': y3,
    'fitted': r3.fittedvalues,
    'pred': pred3
}).plot(legend=True)

效果如图：

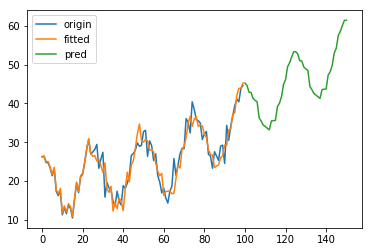
3.2 Holt-Winters’ multiplicative method

乘法模型形如：

Forecast equation: y^t+h∣t=(lt+hbt)st+h−m(k+1)\hat{y}_{t+h|t} = (l_t + hb_t)s_{t+h-m(k+1)}
Level equation: lt=αytst−m+(1−α)(lt−1+bt−1)l_t = \alpha\dfrac{y_t}{s_{t-m}} + (1-\alpha)(l_{t-1} + b_{t-1})
Trend equation: bt=β(lt−lt−1)+(1−β)bt−1b_t = \beta(l_t - l_{t-1}) + (1-\beta)b_{t-1}
Seasonal equation: st=γyt(lt−1+bt−1)+(1−γ)st−ms_t = \gamma\dfrac{y_t}{(l_{t-1} + b_{t-1})} + (1-\gamma)s_{t-m}

效果如图：

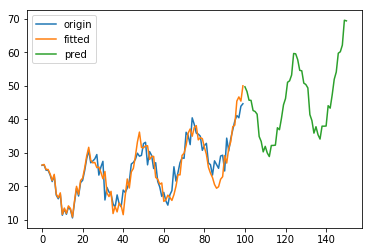
3.3 Holt-Winters’ damped method

Holt-Winters’ 模型的趋势部分同样可以引入阻尼系数 ϕ\phi，这里不再赘述。

4. 参数优化和模型选择

参数优化的方法是最小化误差平方和或最大化似然函数。模型选择可以根据信息量准则，常用的有 AIC 和 BIC等。

AIC 即 Akaike information criterion， 定义为

AIC=2k−2ln⁡L(θ)AIC = 2k - 2\ln L(\theta)

其中 L(θ)L(\theta) 是似然函数， kk 是参数数量。用 AIC 选择模型时要求似然函数大，同时对参数数量作了惩罚，在似然函数相近的情况下选择复杂度低的模型。

BIC 即 Bayesian information criterion，定义为

BIC=kln⁡n−2ln⁡L(θ)BIC = k\ln n - 2\ln L(\theta)

其中 nn 是样本数量。当 n>e2≈7.4n>\mathrm{e}^2\approx 7.4 时，kln⁡n>2kk\ln n > 2k，因此当样本量较大时 BIC 对模型复杂度的惩罚比 AIC 更严厉。

5. 与 ARIMA 的关系

线性的指数平滑方法可以看作是 ARIMA 的特例。例如简单指数平滑等价于 ARIMA(0, 1, 1)，Holt’s linear trend method 等价于 ARIMA(0, 2, 2)，而 Damped trend methods 等价于 ARIMA(1, 1, 2) 等。

我们不妨来验证一下。

lt=αyt+(1−α)lt−1l_t = \alpha y_t + (1-\alpha)l_{t-1} 可以改写为

y^t+1=αyt+(1−α)y^t=αyt+(1−α)(yt−ϵt)=yt−(1−α)ϵt\hat y_{t+1} = \alpha y_t + (1-\alpha)\hat y_t = \alpha y_t +(1-\alpha)(y_t-\epsilon_t) = y_t - (1-\alpha)\epsilon_t

亦即

y^t=yt−1−(1−α)ϵt−1\hat y_t = y_{t-1} -(1-\alpha) \epsilon_{t-1}

两边同时加上 ϵt\epsilon_t，得

yt=y^t+ϵt=yt−1+ϵt−(1−α)ϵt−1y_t = \hat y_t + \epsilon_t = y_{t-1} + \epsilon_t - (1-\alpha)\epsilon_{t-1}

而 ARIMA(p, d, q) 可以表示为

(1−∑i=1pϕiLi)(1−L)dXt=(1+∑i=1qθiLi)ϵt\left(1-\sum\limits_{i=1}^p\phi_iL^i\right)(1-L)^dX_t = \left(1+\sum\limits_{i=1}^q\theta_iL^i\right)\epsilon_t

其中 LL 是滞后算子（Lag operator），LjXt=Xt−jL^jX_t = X_{t-j}。
考虑 ARIMA(0, 1, 1)

(1−L)Xt=(1+θ1L)ϵt(1-L)X_t = (1 + \theta_1L)\epsilon_t

即

Xt−Xt−1=ϵt+θ1ϵt−1X_t - X_{t-1} = \epsilon_t + \theta_1\epsilon_{t-1}

亦即

Xt=Xt−1+ϵt+θ1ϵt−1X_t = X_{t-1} + \epsilon_t + \theta_1\epsilon_{t-1}

令 θ1=−(1−α)\theta_1=-(1-\alpha)，则两者等价。

非线性的指数平滑方法则没有对应的 ARIMA 表示。

参考文献

[1] Hyndman, Rob J., and George Athanasopoulos. Forecasting: principles and practice. OTexts, 2014.
[2] Exponential smoothing - Wikipedia
[3] Introduction to ARIMA models - Duke